La elaboración, diseño, construcción y fabricación de PCB también llamadas board o Tarjeta de Circuito Impreso es el paso final para culminar nuestros proyectos en electrónica. En este artículo se explica como realizar dicho proceso utilizando el software KidCad.
Este artículo utilizara un proyecto simple de un oscilador astable usando un 555 como ejemplo para el diseño de nuestro PCB.
1. Descargar KiCad, FreeRouting y FreeCAD
Los software que se necesitaran para la Elaboración Diseño Construcción y Fabricación de PCB una nueva placa de circuito impreso son los siguientes:
- KiCad: aquí se realiza todo el diseño del esquemático y se asocian las diferentes huellas, además también genera los diferentes archivos para enviar a fabricación. Se puede descargar aquí.
- FreeRouting: por defecto las rutas en KiCad se deben realizar de forma manual, sin embargo este software nos ayudará a crear las rutas de forma automática y optimizadas. Se puede descargar aquí.
- FreeCad: en caso de tener elementos o componentes que no posean modelos 3D podemos utilziar este software para construir los modelos y luego usarlos en KiCad. Se puede descargar aquí.
2. Primer paso – Creación del proyecto
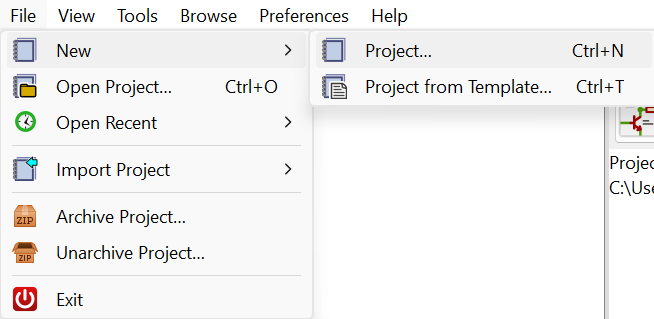
El primer paso para diseñar un nuevo PBC o Tarjeta de Circuito Impreso es crear un nuevo proyecto. Este paso es bastante simple y solo requiere que se seleccione una carpeta y asignar un nombre mediante la opción “nuevo proyecto” en el menú.
3. Segundo paso – Creación del esquemático
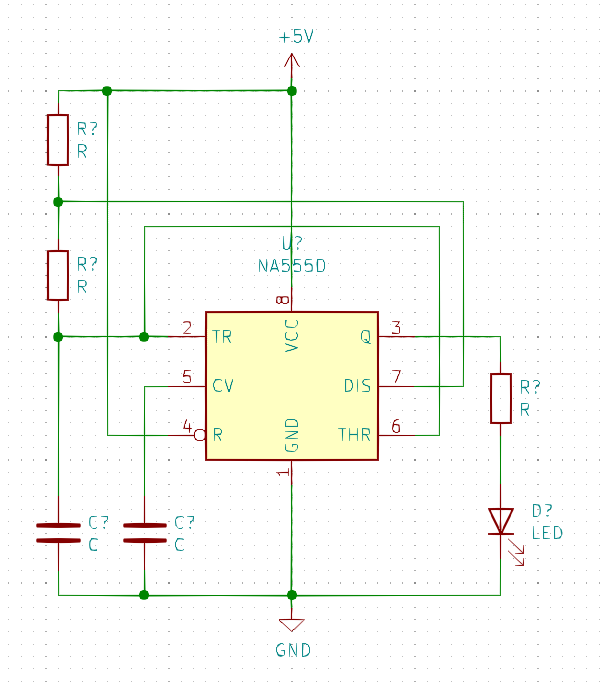
El plano esquemático contiene las diferentes conexiones eléctricas entre los componentes de nuestro circuito. En la figura 1.2 se muestra el diagrama esquemático de nuestro circuito. Es importante considerar las siguientes recomendaciones cuando se diseña el circuito.
- Si se utilizan buses para realizar las conexiones eléctricas, asegurese de usar entradas de cable que salen de los buses y se conectan con otras partes del circuito con cables normales, además de etiquetar cada cable de entrada al bus con una etiqueta de red.
- Compruebe todas las conexiones usando la herramienta de resaltado de red que permitirá verificar las conexiones de forma apropiada de manera que no hayan puntos flotantes, también se puede realizar la comprobación con la herramienta “ejecutar reglas de conexión eléctrica”.
- En la herramienta de configuración de página establezca valores adecuados que rellenaran el cajetín de la hoja del esquemático. Tenga en cuenta que se puede configurar su propio cajetín o agregar imágenes o logos que desee incluir a las librerías del proyecto y personalizar los diseños.
- Tenga presente que si no encuentra un símbolo en las librerías predefinidas se puede descargar y agregar, la siguiente web contiene la mayoría de símbolos snapeda.
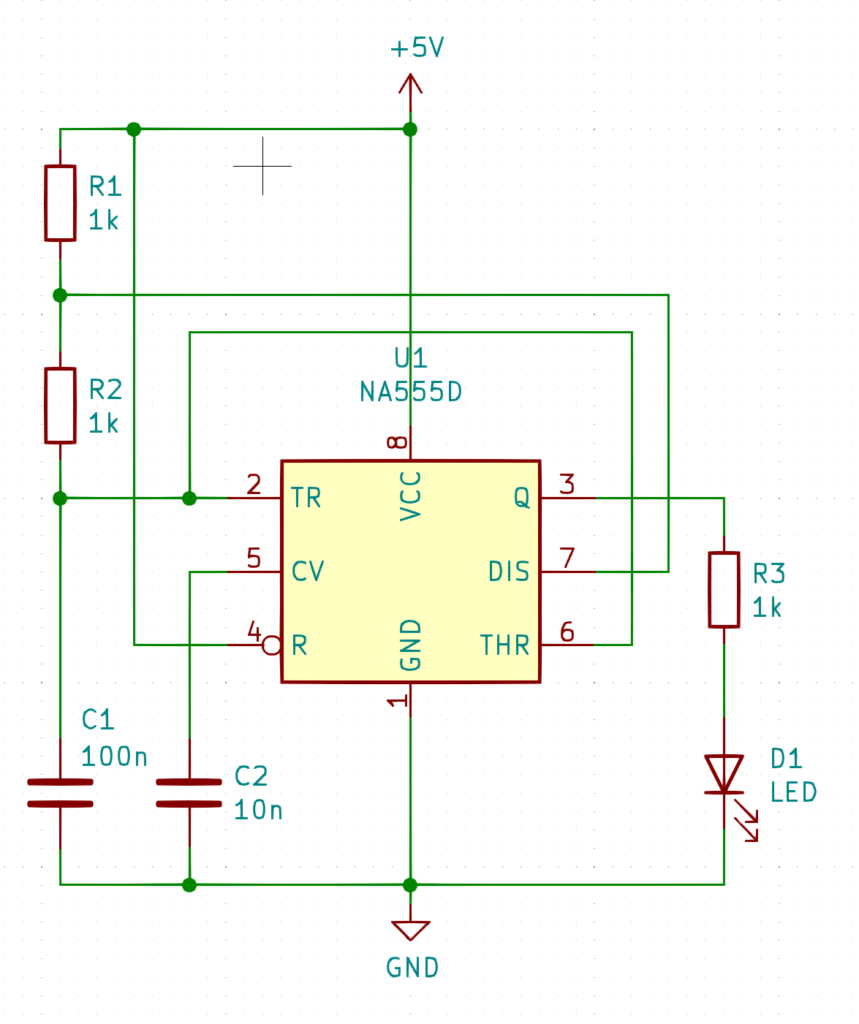
El paso siguiente será dar valor a cada componente y numerarlos, para ello podemos ir componente a componente y dando doble click establecer sus valores. Para la enumeración podemos usar la herramienta Anotar valores de símbolos lo cual numerará de forma automática los componentes. El resultado final del esquemático se muestra en la figura 1.3.
4. Tercer paso – Asociar los footprints y generar lista de redes
En la Elaboración Diseño Construcción y Fabricación de PCB el siguiente paso implica asignar los footprints a los diferentes componentes, en caso que no exista un footprint se puede buscar en la web o en su defecto diseñar el componente usando software como FreeCad.
Es muy recomendable que siempre se realice la verificación de cada footprint e incluso se verifique su modelo 3D con el cual se puede corroborar que se esta usando el footprint correcto.
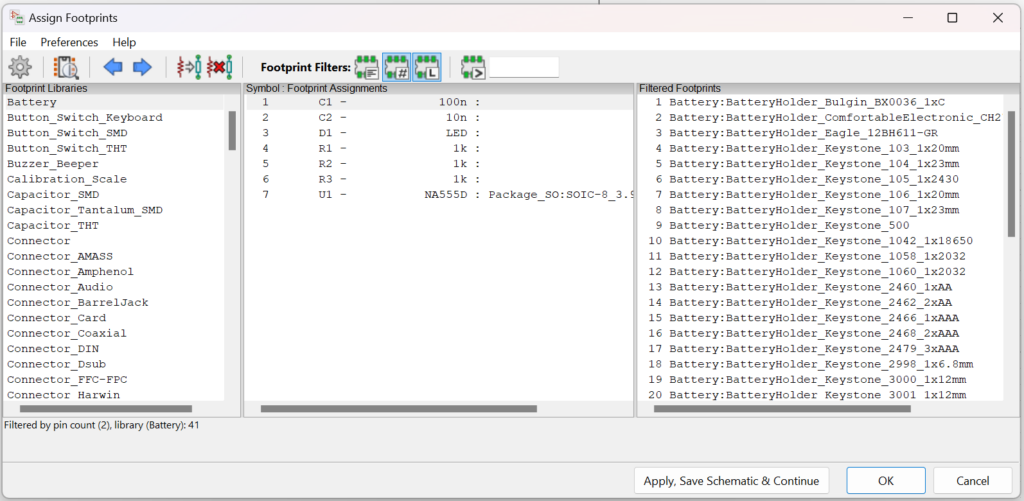
Una vez hecho este paso, se puede realizar la exportación de la lista de redes lo cual es necesario para poder diseñar el circuito impreso y sus rutas, de hecho el software de auto ruteo necesita como entrada el archivo de lista de redes.
5. Generación del circuito impreso y sus rutas
El primer paso antes de continuar consiste en cargar las lista de redes en la herramienta PCBnew, esta operación cargará los footprint y el esquemático con lo cual se puede proceder a crear las rutas de forma manual o automática. Tenga en cuenta que se pueden crear vías para pasar entre diferentes capas de cobre.
La figura 5 muestra la carga inicial de las redes en la herramienta PCBnew de KiCad, si se desea continuar de forma manual se puede ubicar los componentes adecuadamente y posteriormente reemplazar las líneas que representan cables por pistas que unan los componentes de forma eléctrica.
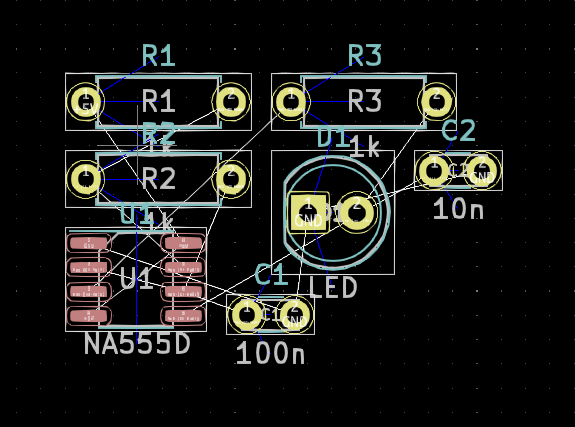
Luego de ubicar y rotar los elementos correctamente a sus posiciones definitivas se puede continuar con el proceso de ruteo que a continuación se explica usando una herramienta automática.
Si se desea realizar un ruteo automático debemos cambiar de programa, abrir freerouting (el aplicativo java se encuentra en la carpeta de instalación) y luego debe seleccionar el archivo Specctra DSN exportado previamente de KiCad.
Algunos preparativos importantes incluyen:
- Revisar los colores y capas en el menú utilities/display/colors
- Revisar las reglas de ruteo en cuanto a los tamaños de las pistas en utilities/rules/net clases
- Asignar reglas de rutas en utilities/rules/nets
Para iniciar el ruteo se puede seleccionar routing/autorouting. Se pueden modificar los parámetros de ruteo como clases a fin de volver a rutear hasta obtener un resultado valido.
La figura 6 muestra el resultado del auto ruteo en el caso de nuestro esquemático.
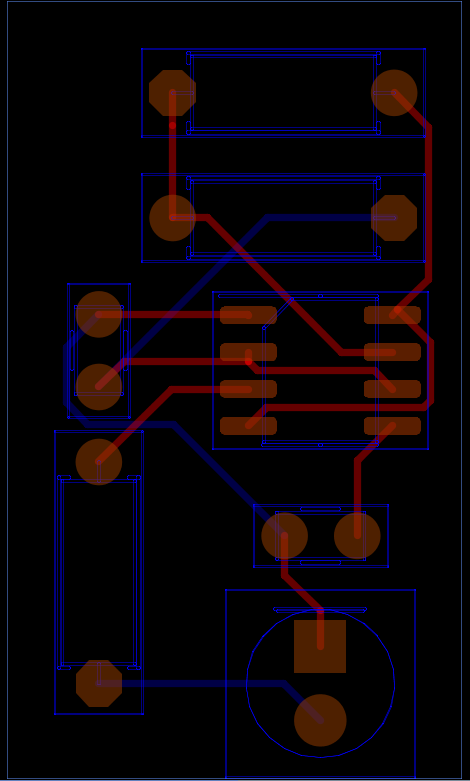
Como paso final se debe exportar el archivo de rutas a través del menú file/export/export specctra session file, este archivo se importa nuevamente en KiCad y con ello ya se tienen las rutas de forma automática. La figura 7 muestra el resultado de este autoruteo aplicado en KiCad que en este caso se realizó a doble capa.
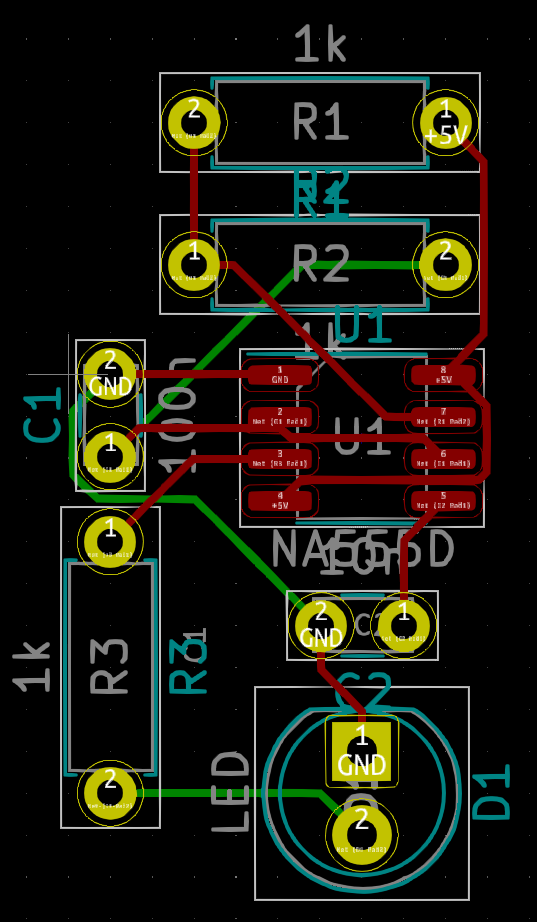
6. Retoques finales al PCB
Teniendo las rutas en KiCad, se puede observar que algunas rutas que pueden ser mejoradas a mano puesto que han pasado muy cerca de otras pistas o pad o que dificultaran el proceso de soldado. Este paso se puede realizar manualmente o modificando las reglas de autoruteo, a continuación se muestra el resultado final con las pistas mejoradas manualmente.
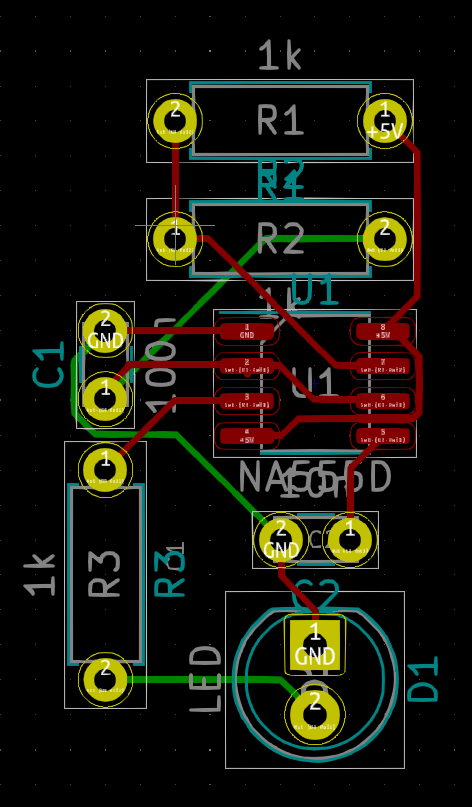
El correspondiente resultado 3D se muestra en la figura 9.

7. Herramientas de optimización y detalles finales
Algunos puntos importantes a considerar para la realización de planos profesionales son los siguientes.
- Incluir en la capa edge.cuts un polígono con el limite de la placa
- Incluir pines de alimentación en la placa.
- Incluir secciones o áreas de cobre para masas o alimentación.
- Incluir tornillos de sujeción de la placa.
8. Generación de archivos para fabricación
Para la Elaboración Diseño Construcción y Fabricación de PCB, la la placa se puede realizar de dos formas diferentes la primera por serigrafia, imprimiendo la capa de rutas y realizando el proceso de impresión sobre placa cobre y luego aplicando acidos. Sin embargo, existe otro mecánismo mucho más simple enviando a fabricación externa en paginas como la de JLCPCB y otras muchas empresas que se encargan de fabricar PCB.
Para ello basta con seleccionar la herramienta plot seleccionar todas las capas y generar los archivos gerber, hay que tener en cuenta que en KiCad existe una opción adicional para generar el archivo de taladros necesarios para enviar a fabricación. Una vez generado los archivos, lo cual se recomienda generarlos en una carpeta aparte, se requerira comprimir en ZIP y seguir los pasos para subirlos y enviar a fabricación en la empresa seleccionada.
Para finalizar una recomendación final es que en cada paso existen multitud de opciones y herramientas que ayudaran a construir el diseño de forma detallada, algunas recomendadas son:
- Incluir planos de masa o alimentación para mejorar interferencias EMI.
- Incluir mounting holes.
- Incluir arcos o bordes redondeados en los limites de la placa.