Categoría: Matemáticas (Página 1 de 3)

El Cálculo Vectorial es una de las ramas con más aplicaciones del cálculo, permite calcular flujos y entender muchos fenómenos físicos que han sido modelados con esta potente herramienta. En esta entrada se abordan los diferentes conceptos clave y teoremas que han sido resultado de esta rama de las matemáticas.

Si quieres aprender desde cero temas básicos de cálculo puedes seguir este enlace.

1. Campos escalares y vectoriales

Un campo vectorial es una función $F$ que asigna a un punto en $\mathbb R^2$ o $\mathbb R^3$ un vector. Este campo se puede escribir como:

$\mathbf F=P(x,y)\mathbf i +Q(x,y)\mathbf j$

Donde las funciones $P$ y $Q$ se conocen como campos escalares.

1.1. Campos gradientes

Si verificamos nuevamente la definicion de gradiente, encontramos que esta dado por:

$\nabla f(x,y)=f_x(x,y)\mathbf i+f_y(x,y)\mathbf j$

Por lo cual se puede apreciar que el campo gradiente en realidad es un campo vectorial.

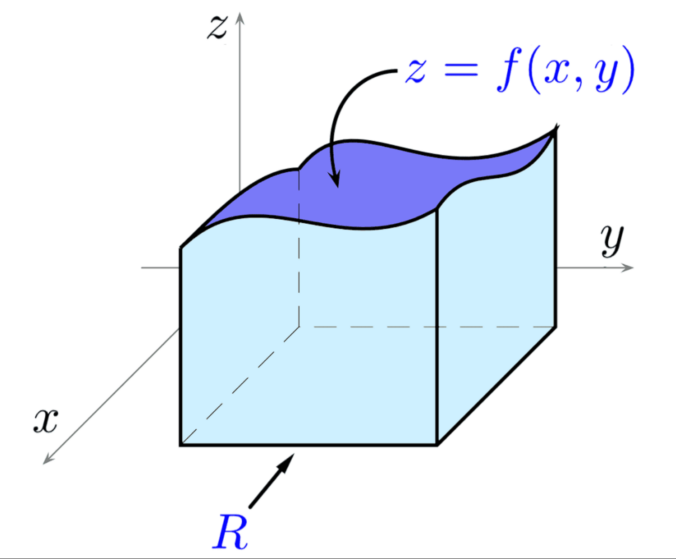
Note que el campo gradiente de una función $f(x,y)$, que corresponde a una superficie en el espacio, es un campo en el plano, donde cada vector señala la máxima dirección de crecimiento de la superficie en el espacio.

2. Integrales de línea

Las integrales de superficies se pueden calcular caudndo en el plano se tiene una region $D$ sobre la cual se quiere integrar o cuando se integra sobre uno de los ejes. Sin embargo es posible encontrar una integral de línea o también conocida como de curva o cortina dado una curva en el plano y la respectiva superficie a integrar, es algo similar a calcular el a´rea bajo la curva en el plano proyectada sobre la superficie a integrar.

La siguiente ecuación permite realizar el cálculo de esta integral de línea.

$\int_c f(x,y)ds=\int_a^bf(x(t),y(t))\sqrt{(\frac{dx}{dt})^2+(\frac{dyt}{dy})^2}dt$

Note como la superficie a integrar ha sido escrita como una parametrización de $t$ y que además la integral de la raíz cuadrada cooressponde a la longitud de arco.

En caso que las integrales de línea se calculen sobre los ejes $x$ e $y$ podemos escribir:

$\int_c{(x,y)}dx+\int_c{Q(x,y)}dy=\int_c{P(x,y)dx+Q(x,y)dy}$

Note que este caso no se parametrizó la superificie.

La parametrización de la superficie puede ser el mayor reto, en ocasiones es conveniente recordar la parametrización de un segmento de línea que comienza en $\mathbf r_0$ y termina en $\mathbf r _1$, con $0 \leq t \leq 1$:

$\mathbf r(t)=(1-t)\mathbf r_0+t\mathbf r_1$

En general, la parametrización determina una orientación de la curva $C$ en la dirección positiva que corresponde a un incremento del parametro $t$

2.1. Integrales de línea de campos escalares y vectoriales

Las integrales mencionadas anteriormente requieren de una curva en el plan y una superficie en el espacio, sin embargo las integrales de línea también se pueden calcular si se tiene en el plano un campo vectorial y una curva $C$ sobre el mismo dada por la función vectorial $\mathbf r(t)$ con $a \leq t \leq b$. Esta integral de línea a lo largo de $C$ se escribe así:

$\int_C \mathbf F \cdot d\mathbf r=\int_a^b{\mathbf F(\mathbf r(t)) \cdot \mathbf r'(t)dt}=\int_C\mathbf F \cdot \mathbf T ds$

Note que $\mathbf F(\mathbf r(t)$ es una forma abreviada de escribir $\mathbf F(x(t),y(t),z(t))$.

Así mismo, se puede obtener las siguiente relación entre las integrales de linea sobre campos vectoriales e integrales de línea de campos escalares.

$\int_c \mathbf F \cdot d\mathbf r=\int_C Pdx+Qdy+Rdz$

Con $\mathbf F=P\mathbf i + Q\mathbf j + R\mathbf k$

Interpretación: en este caso note que la integral de línea no es un área bajo la curva, en este caso, si $\mathbf F$ y $\mathbf r$ que es el vector que representa la curva, si ambos estan en el plano, esta integral de línea del producto punto del campo vectorial y el vector que describe la curva se puede interpretar como la suma delas contribuciones infinitesimales de cada producto punto entre el campo vectorial y el cetor de la curva para cada punto sobre la curva.

2.2. Teorema fundamental de las integrales de línea

Este teorema establece que si la integral del línea del campo vectorial, corresponde a un campo vectorial gradiente, solomante es necesario obtener la diferencia de los valores de la función en los extremos de la curva:

$\int_c\nabla f\cdot \mathbf r=f(\mathbf r(b))-f(\mathbf r(a))$

2.3. Independencia de la trayectoria

Del teorema anterior se desprenden algunas consecuencias importantes y definiciones que se recopilan a continuación.

En primer lugar, se establece la independencia de la trayectoria, es decir, el resultado de la intelgral de línea no depende de la curva, si en una región $D$:

$\int_C\mathbf F \cdot d\mathbf r=0$

para toda trayectoria cerrada $C$ en $D$.

Además, si $\mathbf F$ es un campo vectorial continuo en una region abierta y conexa $D$. Si $\int_C\mathbf F\cdot d\mathbf r$ es independiente de la trayectoria en $D$ entonces se dice que $\mathbf F$ es un campo vectorial conservativo sobre $D$, en otras palabras existe la función potencial $f$ que genera $\nabla f=\mathbf F$.

Adicionalmente, si $\mathbf F=P(x,y)\mathbf i + Q(x,y)\mathbf j$ es un campo vectorial conservativo y $P$ y $Q$ tienen derivadas parciales de primer orden continuas sobre un dominio $D$ entonces:

$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$

Definamos una curva simple como aquella que no se cruza a si misma, adicionalmente podemos definir curvas simples abiertas y cerradas y una región simplemente conexa si la región no tiene “huecos”.

Con $\mathbf F=P(x,y)\mathbf i + Q(x,y)\mathbf j$ un campo vectorial sobre una region abierta simplemente conexa en $D$ y con $P$ y $Q$ con derivadas parciales de primer orden continuas y además:

$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$

Entonces, $\mathbf F$ es conservativo.

3. Teorema de Green

El teorema de Green establece una relación entre las integrales de línea, cuando la curva sobre la que se integra encierra una área y una integral doble sobre esa área. En este sentido, la región encerrada por la curva debe ser recorrida por el vector $\mathbf r$ en sentido antihorario, siendo esta la convención conocida como orientación positiva de la región.

$\int_C\mathbf F \cdot d \mathbf r= \int_C Pdx+Qdy = \iint_D(\frac{\partial Q}{\partial X}-\frac{\partial P}{\partial y})dA$

Este teorema se considera como una extensión del teorema fundamental del cálculo y la integral anterior se puede escribir como sigue a continuacion para indicar que la integral de línea se calcula sobre la orientación positiva de la curva cerrada $C$.

$\oint_C Pdx+Qdy$

El teorema de Green provee la siguiente formula para el cálculo del área:

$A=\oint_C xdy=-\oint_C ydx=\frac{1}{2}\oint_C xdy-ydx$

4. Rotacional y Divergencia

Rotacional

El rotacional es una operación sobre vectores que produce un campo vectorial y que se escribe usando el producto cruz de las operaciones con vectores. La forma de calcular el rotacional y su notación se muestra a continuación.

$rot \mathbf F=\nabla \times \mathbf F=(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z})\mathbf i+(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x})\mathbf j+(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})\mathbf k$

Note que el operador nabla, que se uso para describir el vector gradiente se puede entender como la siguiente operacion:

$\nabla=\mathbf i\frac{\partial}{\partial x} + \mathbf j\frac{\partial}{\partial y} + \mathbf k\frac{\partial}{\partial z}$

Algunos resultados del rotacional implica lo siguiente:

• El rotacional del gradiente es cero: $\nabla \times (\nabla f) = 0$
• Un campo vectorial con derivadas parciales continuas y si $\nabla \mathbf F = 0$ entonces $\mathbf F$ es un campo vectorial conservativo.

Divergencia

Esta operación produce un campo escalar y usa el producto punto de las operaciones vectoriales. Se define como se muestra a continuación:

$\nabla \cdot \mathbf F=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}$

En este caso si el campo vectorial tiene derivadas parciales continuas de segundo orden entonces:

$\nabla \cdot \nabla \times \mathbf F=0$

Teorema de Green

Usando las operaciones vectoriales se puede volver a escribir el teorema de Green usando el rotacional y la divergencia:

$\oint_C \mathbf F \cdot d\mathbf r=\iint_D(\nabla \times \mathbf F) \cdot \mathbf k dA$

$\oint_C \mathbf F \cdot \mathbf n ds=\iint_D(\nabla \cdot \mathbf F) dA$

5. Integrales de Superficie

las integrales de superficie son el equivalente de las integrales de línea pero en una dimensión superior, en este caso las integrales de superficie permiten calcular las sumatoria de las contribuciones de un campo vectorial a través de una superficie, lo cual se puede escribir así:

$\iint_S f(x,y,z)dS = \iint_D f(\mathbf r(u,v))|\mathbf r_u \times \mathbf r_v|dA$

Observe que esta no es la misma área superficial, así como la integral de línea no es el área bajo la superficie delimitada por la curva. Estas integrales son muy utilizadas en cálculos de campos y flujos como los electromagnéticos.

Si la parametrización es $x=x$, $y=y$ y $z=g(x,y)$ esta integral de superficie es:

$\iint_S f(x,y,z)dS = \iint_D f(x,y,g(x,y))\sqrt{(\frac{\partial z}{\partial x})^2+(\frac{\partial z}{\partial y})^2+1}dA$

La integral de superficie para campos vectoriales requerira el vector normal unitario a la superficie, que para una superficie cerrada la convencio es que estos vecotores son positivos cuando apuntan hacia afuera de la superficie, esto se conoce como orientación positiva de la superficie. Con:

$\mathbf n=\frac{\mathbf r_u \times \mathbf r_v}{|\mathbf r_u \times \mathbf r_v|}$

Se puede calcular las integrales de superficie usando los siguientes resultados:

$\iint_S \mathbf F \cdot d\mathbf S=\iint_S\mathbf F \cdot \mathbf n dS$

$\iint_S \mathbf F \cdot d\mathbf S=\iint_D\mathbf F \cdot (\mathbf r_u \times \mathbf r_v) dA$

$\iint_S \mathbf F \cdot d\mathbf S=\iint_D (-P\frac{\partial g}{\partial x}-Q\frac{\partial g}{\partial y}+R) dA$

6. Teorema de Stokes

El teorema de Stokes se puede considerar un equivalente del teorema de Green pero para una dimensión más alta al relacionar una integral de liena con una integral de superficie.

Sea $S$ una superficie orientada y suave a segmentos, acotada por una curva frontera $C$ suave a segmentos, cerrada y simple, con orientaciones positivas y $\mathbf F$ un campo vectorial con derivadas parciales continuas sobre la región que contiene a $S$ entonces:

$\int_C\mathbf F \cdot d\mathbf r=\iint_S \nabla \times \mathbf F \cdot d \mathbf S$

7. Teorema de la Divergencia

Similar al teorema de Stokes el teorema de la divergencia relaciona la integral de superficie con una integral tripe sobre un volumen. Observe que son variaciones de los diferentes resultados de las operacioens vectoriales de las integrales pero en dimensiones más altas.

$\iint_S\mathbf F \cdot d\mathbf S=\iiint_E \nabla \cdot F dV$

8. Artículos de Interes

Geometría Vectorial

Integrales Dobles y Triples

Derivadas Parciales en Varias Variables

Las Integrales Dobles y Triples son la aplicación del concepto de Integral al cálculo de múltiples variables, estas integrales aparecen frecuentemente en muchos campos como probabilidad, centros de masa, cálculo de volúmenes y un sin fin de aplicaciones a física y otras ramas del conocimiento.

Si quieres aprende sobre integrales puedes comenzar aquí.

1. Definición de integral doble

Esta definición de integral doble es bastante fácil de entender pues es simplemente la extensión a varias variables de la integral sencilla. Aquí es conveniente recordar que la integral de una variable es el área de la curva formada por la suma de rectangulos y haciendo que el ancho de estos rectangulos tienda a cero, similarmente con dos variables sería el volumen bajo la superficie determinado por:

$\iint_R{f(x,y)dA}=\lim_{m,n\to\infty}\sum_{i=1}^m{\sum_{j=1}^n}f(x_i,y_i)\delta A$

A la parte derecha de la ecuación anterior se le conoce como la Suma de Riemann. Si la función es positiva $f(x,y)>0$ se puede interpretar la integral como el volumen:

$V=\iint_R{f(x,y)dA}$

Similar al caso de una variable podemos encontrar el valor promedio de una función de dos variables usando:

$f_{prom}=\frac{1}{A(R)}\iint_R{f(x,y)dA}$

2. Propiedades de la Integrales dobles

Las integrales múltiples cumplen las mismas propiedades de las integrales simples:

• $\iint[f(x,y)+g(x,y)]dA=\iint f(x,y)dA+\iint g(x,y)dA$
• $\iint cf(x,y)dA=c\iint f(x,y)dA$
• Si $f(x,y) \ge g(x,y)$ entonces $\iint f(x,y)dA \ge \iint g(x,y)dA$
• Si $m \le f(x,y) \le M$ se cumple en el dominio de integracion $D$ entonces $mA(D) \le \iint_D{f(x,y)dA} \le MA(D)$

3. Integrales iteradas y Teorema de Fubini

Para calcular integrales dobles se puede realizar el cálculo de una de las integrales primero que la otra de forma iterada, elegir cual variable se integra primero conduce a que sea más fácil calcular la segunda. El Teorema de Fubini establece que el orden en que se calculan las derivadas produce el mismo resultado.

Sea $f$ continua en $R={(x,y)|a \le x\le b, c \le y \le d}$ entonces

$\iint_R{f(x,y)dA}=\int_a^b\int_c^d{f(x,y)dydx}=\int_c^d\int_a^b{f(x,y)dxdy}$

Una consecuencia del Teorema de Fubini que puede simplificar el cálculo de algunas integrales es si la función se puede dividir como dos funciones exclusivamente de $x$ y $y$:

$\iint_R{g(x)h(y)dA}=\int_a^b{g(x)dx}\int_c^d{h(y)dy}$

4. Integrales dobles sobre regiones generales

En las integrales definidas anteriormente, la región de integración corresponde a un rectangulo sobre el plano $XY$, sin embargo se puede realizar integrales sobre regiones más generales definidas por curvas dependintes de $x$ (regiones tipo I) o curvas dependientes de $y$ (regiones tipo II).

A continuación se muestran las ecuaciones para calcular estas integrales.

Para regiones tipo I:

$D={(x,y) \in a \le x \le b, g_1(x) \le y \le g_2(x)}$

$\int_D{f(x,y)dA}=\int_a^b\int_{g_1(x)}^{g_2(x)}{f(x,y)dydx}$

Para regiones tipo II:

$D={(x,y) \in c \le y \le d, h_1(x) \le x \le h_2(x)}$

$\int_D{f(x,y)dA}=\int_c^d\int_{h_1(x)}^{h_2(x)}{f(x,y)dxdy}$

También es importante notar que una región más general se puede partir y obtener la integral como la suma de las integrales así:

Si $D = D_1 \cup D_2$ entonces:

$\iint_D{f(x,y)dA}=\iint_{D_1}{f(x,y)dA}+\iint_{D_2}{f(x,y)dA}$

4.1. Integrales dobles en coordenadas polares

Para realizar una integral en coordenadas polares puede utilizarse el siguiente cambio de variable:

Si $f$ es continua en un rectangulo polar dado por $R$ tal que $0 \le a \le r \le b$ y $\alpha \le \theta \le \beta$ y $0 \le \beta – \alpha \le 2 \pi$ entonces:

$\iint_R{f(x,y)dA}=\int_\alpha^\beta\int_a^b{f(r\cos\theta,r\sin\theta)rdrd\theta}$

Note que también puede integrar sobre funciones que definan los arcos similar al caso de integrales sobre regiones generales en coordenadas rectangulares.

5. Aplicaciones de Integrales dobles

Algunas de las aplicaciones más comunes de integrales dobles se muestran a continuación, estas aplicaciones fácilmente pueden ser extendidas a más de dos dimensiones utilizando integrales triples.

5.1. Masa

Dada la densidad, que es la masa por unidad de área y si esta densidad es variable se puede utilizar esta definición para calcular la masa usando:

$m=\iint_D{\rho(x,y)dA}$

5.2. Momentos

Los momentos de masa se pueden entender desde su aplicación que permite obtener el centro de masa de una lámina, estos centros de masa equivalen al punto donde la lámina se equilibra y es equivalente a tener toda la mas ubicada en ese punto, a continuación se dan las ecuaciones de los momentos y centros de masa de una lámina con densidad variable.

$M_x=\iint_D{y\rho(x,y)dA}$

$M_y=\iint_D{x\rho(x,y)dA}$

Y el centro de masa:

$\bar x=\frac{1}{m}\iint_D{x\rho(x,y)dA}$

$\bar y=\frac{1}{m}\iint_D{y\rho(x,y)dA}$

Los segundos momentos son conocidos así pues representan el momento de inercia de la lámina, a continuación se muestran estos momentos respecto a los ejes y al origen, este último también se conoce como momento polar de inercia:

$I_x=\iint_D{y^2\rho(x,y)dA}$

$I_y=\iint_D{x^2\rho(x,y)dA}$

$I_0=\iint_D{(x^2+y^2)\rho(x,y)dA}$

5.2. Área Superficial

El área de una superficie se puede calcular con el uso de integrales dobles, si tenemos la representación paramétrica de la superficie:

$\mathbf r=x(u,v)\mathbf i + y(u,v) \mathbf j + z(u,v) \mathbf k$

Entonces el área superficial esta definida por:

$A(S)=\iint_D{1\mathbf r_u \times \mathbf r_v| dA}$

Donde

$\mathbf r_u=\frac{\partial x}{\partial u}\mathbf i + \frac{\partial y}{\partial u} \mathbf j + \frac{\partial z}{\partial u} \mathbf k$

$\mathbf r_v=\frac{\partial x}{\partial v}\mathbf i + \frac{\partial y}{\partial v} \mathbf j + \frac{\partial z}{\partial v} \mathbf k$

Alternativamente se puede calcular como:

$A(S)=\iint_D{\sqrt{1+\frac{\partial z}{\partial x}^2+\frac{\partial z}{\partial y}^2}dA}$

6. Integrales triples

Las integrales triples son muy parecidas a las integrales dobles excepto que existe una variable adicional, además aplican las mismas reglas y principios. En este caso no existe una interpretación gráfica como tal ya que la región de integración es un volumen y se esta integrando una función de tres variables cuyos valores se requerirían dibujar en el hiperespacio cuadridimensional.

El teorema de Fubini aplica de igual manera y las regiones de integración no necesariamente deben ser cubos, sino que pueden ser funciones que acoten la región.

En general la integral de tres variables se define con sumas de Reimann y se puede escribir como:

$\iiint_B{f(x,y,z)dV}=\int_r^s\int_c^d\int_a^b{f(x,y,z)dxdydz}$

Para regiones generales se puede establecer integrales como la siguiente:

$\iiint_B{f(x,y,z)dV}=\int_a^b\int_{g_1(x)}^{g_2(x)}\int_{u_1(x,y)}^{u_2(x,y)}{f(x,y,z)dxdydz}$

6.1. Integrales triples en coordenadas cilíndricas

El cambio de variable para coordenadas cilíndricas en integrales triples arroja el siguiente resultado:

$\iiint_B{f(x,y,z)dV}=\int_\alpha^\beta\int_{h_1(\theta)}^{h_2(\theta)}\int_{u_1(r\cos\theta,r\sin\theta)}^{u_2(r\cos\theta,r\sin\theta)}{f(r\cos\theta,r\sin\theta,z)rdzdrd\theta}$

6.2. Integrales triples en coordenadas esféricas

El cambio de variable para coordenadas esféricas en integrales triples arroja el siguiente resultado:

$\iiint_B{f(x,y,z)dV}=\int_c^d\int_\alpha^\beta\int_a^b{f(\rho\sin\phi\cos\theta,\rho\sin\phi\sin\theta,\rho\cos\phi)\rho^2\sin\phi d\rho d\theta d\phi}$

7. Cambio de variables y Jacobiano

La transformación o cambio de una variable cuando la integral es de una sola variable se puede realizar de la siguiente manera:

$\int_a^b{f(x)dx}=\int_c^d{f(g(u))g'(u)du}$

La equivalencia entre los límites esta dada por $x=g(u)$ es decir $a=g(c)$ y $b=g(d)$.

En el caso de dos o más variables, también se puede realizar cambios de variables, como el de coordenadas polares, cilíndricas o esféricas. Para realizar este cambio debemos comprender que se esta transformando la región original de integración en una nueva y que para ello denotamos el nuevo plano y los nuevos límites con nombres de variables diferentes. Así mismo, definimos que una transformación $T$ es una $transformacion C^{-1}$ lo cual indica que las funciones de transformación $g$ y $h$ tienen derivadas parciales continuas.

$x=g(u,v)$

$y=h(u,v)$

Las nuevas variables son $u$ y $v$ y el la región original $R$ se llamará ahora $S$.

En general integrar realizando un cambio de variables en dos o más variables es conveniente definir el siguiente determinante que se conoce como el jacobiano:

$\frac{\partial (x,y)}{\partial (u,v)}=\left| \begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial x}{\partial v} \end{array} \right|=\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial x}{\partial v}\frac{\partial y}{\partial u}$

Con esta definición el cambio de variables en dos variables se puede escribir como:

$\iint_R{f(x,y)dA}=\iint_S{f(x(u,v),y(u,v))|\frac{\partial (x,y)}{\partial (u,v)}|dudv}$

8. Artículos de Interés

Geometría Vectorial

Sistemas de Coordenadas

Técnicas de Integración en Cálculo

Luego de estudiar las derivadas en una sola variable y en general el cálculo en una sola variables, la extensión natural surge cuando consideramos funciones de más de una variable y por lo tanto también aparece la posibilidad de obtener Derivadas Parciales en Varias Variables, las consideraciones más importantes se recopilan en este post.

Para aprender derivadas en una sola variable sigue este link.

1. Funciones varias variables

Las funciones de dos variables se representan como superficies en el espacio tridimensional y depende de dos variables. El dominio y el rango de estas funciones es similar al caso de funciones de una sola variable.

Alternativamente, las funciones de dos variables se pueden representar como curvas en el plano usando las denominadas curvas de nivel que son aquellas curvas para las cuales las funciones de dos variables asumen el mismo valor, esta aproximación es bastante usada en cartografía. Las curvas de nivel están dadas por:

$f(x,y)=k$

También pueden existir funciones de más de dos variables en cuyo caso no se puede obtener una representación gráfica, a lo sumo se puede obtener superficies de nivel y dibujar estas superficies en el espacio tridimensional.

2. Límites y Continuidad

En el caso de varias variables se puede expresar:

$\lim_{(x,y)\to {(a,b)}} f(x,y)=L$

Entonces podemos acercar el valor del límite a $L$ tanto como queramos, acercado lo suficiente $(x,y)$ a $(a,b)$ pero sin que sean iguales.

En el caso de varias variables hay una diferencia con una sola variable y es que para aproximarnos a un punto en el caso de una sola variable solo habían dos opciones o por la izquierda o por la derecha, sin embargo en el caso de varias variables tenemos infinitas opciones o trayectorias, un límite no existe si los valores de los límites por trayectorias diferentes difieren. Dado que no es posible demostrar que un límite exista para todas las trayectorias, se pueden usar alternativas como el teorema del emparedado para demostrar la existencia de estos límites.

Adicionalmente, si el límite existe en un punto $(a,b)$ se dice que la función es continua. Hay que tener presente que la función también puede ser continua en todo el dominio o un subconjunto del dominio.

3. Derivadas parciales

Para realizar una derivada parcial de una función $f(x,y)$ respecto de $x$ simplemente se debe derivar siguiendo las mismas reglas del caso de una variable y tomando $y$ como constante, en este caso se encontrará la pendiente de la superficie y el plano reticular $x$. Similarmente se puede realizar la derivada parcial respecto a $y$.

Para representar la derivada parcial de $x$ se puede usar las siguientes notaciones

$f_x(x,y)=f_x=\frac{\partial f}{\partial x}=\frac{\partial}{\partial x}f(x,y)=\frac{\partial z}{\partial x}=f_1=D_1f=D_xf$

En el caso de más de dos variables la derivada parcial opera en la misma forma que este caso, se toma la variable respecto de la cual se desea derivar y se dejan fijas el resto de variables.

También es posible realizar derivadas de orden superior simplemente tomando la derivada correspondiente del resultado previo de derivar. Las derivadas de orden superior se pueden escribir así:

$(f_x)_x=f_{xx}=f_{11}=\frac{\partial}{\partial x}\frac{\partial f}{\partial x}=\frac{\partial^2f}{\partial x^2}$

Cuando aparecen las derivadas de orden superior o segundas derivadas es posible que nos encontremos con las diferentes combinaciones de derivación entre las variables $x$ y $y$, por ejemplo, aquí se muestra la derivada cruzada primero derivando en $x$ y luego en $y$

$(f_x)_y=f_{xy}=f_{12}=\frac{\partial}{\partial y}\frac{\partial f}{\partial x}=\frac{\partial^2f}{\partial y \partial x}$

3.1. Teorema de Clairaut

Este teorema establece una igualdad entre las derivadas cruzadas, siendo $f$ una función continua en un disco $D$ entonces se cumple que:

$f_{xy}=f_{yx}$

3.2. Regla de la cadena en varias variables

La regla de la cadena en varias variables se puede escribir con los siguientes dos casos:

Caso 1:

Una función $z=f(x,y)$ es una función diferenciable de $x$ y $y$, donde $x=g(t)$ y $y=h(t)$ son funciones diferenciables de $t$ Entonces $z$ es una función diferenciable de $t$:

$\frac{dz}{dt}=\frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{dy}{dt}$

Caso 2:

Sea la función $z=f(x,y)$ es una función diferenciable de $x$ y $y$ donde $x=g(s,t)$ y $y=h(s,t)$ son funciones diferenciables de $s$ y $t$:

$\frac{\partial z}{\partial s}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial s}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial s}$

$\frac{\partial z}{\partial t}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial t}$

3.3. Diferenciación implícita

La regla de la cadena permite obtener ecuaciones sencillas para derivadas complejas, se puede obtener la derivada de $y$ respecto a $x$ usando

$\frac{dy}{dx}=-\frac{F_x}{F_y}$

4. Aproximaciones lineales

En el cálculo de una variable una de las ideas más importantes es que a medida que nos acercamos a un punto la gráfica se parece cada vez más a una línea recta lo cual permite obtener simplificaciones de funciones alrededor de ese punto. En el cálculo de varias variables sucede lo mismo, excepto que la aproximación esta dada por un plano tangente y no por una recta.

Si $f$ tiene derivadas parciales continuas, una ecuación del plano tangente a la superficie $z=f(x,y)$ en el punto $P_0$ es:

$z-z_0=f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)$

A $z$ en la ecuación anterior se le conoce como linealización o aproximación lineal o plano tangente de aproximación de la función $f$.

De la linealización se puede obtener que:

Si las derivadas parciales $f_x$ y $f_y$ existen cerca de $(a,b)$ y son continuas en $(a,b)$ entonces $f$ es diferenciable en $(a,b)$

4.1 Planos tangentes y superficies paramétricas

En el caso que la función (superficie) sea descrita por sus ecuaciones paramétricas:

$\mathbf r(u,v) = x(u,v)\mathbf i+ y(u,v)\mathbf j + z(u,v)\mathbf k$

en el punto $P_0$ dado por $\mathbf r(u_0,v_0)$ se puede obtener dos vectores tangentes a este punto usando derivadas parciales

Con $\mathbf r(u_o,v)$

$\mathbf r_v=\frac{\partial x}{\partial v}(u_0,v_0)\mathbf i + \frac{\partial y}{\partial v}(u_0,v_0)\mathbf j + \frac{\partial z}{\partial v}(u_0,v_0)\mathbf k$

Con $\mathbf r(u,v_0)$

$\mathbf r_v=\frac{\partial x}{\partial u}(u_0,v_0)\mathbf i + \frac{\partial y}{\partial u}(u_0,v_0)\mathbf j + \frac{\partial z}{\partial u}(u_0,v_0)\mathbf k$

Si $\mathbf r_u \times \mathbf r_v$ no es \mathbf 0$ se dice que la superficie es suave y un plano tangente contiene estos dos vecores.

5. Derivadas direccionales y Vector gradiente

Hasta el momento las derivadas parciales han sido respecto a una de las variables independientes de la función. Es posible calcular la derivada en cualquier dirección, no solamente en las direcciones de $x$ o $y$ para ello es necesario contar con el vector unitario que da la dirección en la cual queremos calcular la derivada $\mathbf u = $. En este caso se obtendra la pendiente de la superficie cortada por la reticula en la dirección del vector.

Para calcular la derivada direccional se puede realizar con la siguiente fórmula:

$D_uf(x,y)=f_x(x,y)a+f_y(x,y)b$

El vector gradiente, es un vector especial y muy utilizado en cálculo vectorial y se define como:

$\nabla f(x,y)=\frac{\partial f}{\partial x}\mathbf i + \frac{\partial f}{\partial y}\mathbf j$

Con esta notación podemos reescribir la derivada direccional usando el vector gradiente el producto punto:

$D_uf(x,y)=\nabla f(x,y) \cdot \mathbf u$

La importancia del vector gradiente es debido a que la dirección del vector gradiente corresponde a la mpaxima velocidad de cambio de la superficie correspondiente. Otro hecho destacable es que el vector gradiente es perpendicular a la curva de nivel (o superficie de nivel en el caso de una función de tres variables).

6. Valores Máximos y Mínimos

Una función $f$ tiene un valor máximo o mínimo local en $(a,b)$ y existen las derivadas parciales de primer orden de $f$ entonces $f_x(a,b)=0$ y $f_y(a,b)=0$

En el caso que se cumpla que ambas derivadas sean cero o que alguna de ellas no exista se llama a este un punto crítico o estacionario.

También se puede obtener mediante la prueba de la segunda derivadas información para clasificar los máximos y los mínimos. Si las segundas derivadas son continuas en un disco con centro en $(a,b)$ y este es un punto crítico; sea:

$D=D(a,b)=f_{xx}(a,b)f_{yy}(a,b)-(f_{xy})^2$

• Si $D>0$ y $f_{xx}(a,b)>0, entonces $f(a,b)$ es un mínimo local.
• Si $D>0$ y $f_{xx}(a,b)<0, entonces $f(a,b)$ es un máximo local.
• Si $D<0$ entonces $f(a,b)$ es un punto de silla.

6.1. Máximos y mínimos absolutos

El teorema del valor extremo para funciones de dos variables establece que si $f$ es continua en un conjunto cerrado y acotado $D$ en $\mathbb R^2$ entonces $f$ tiene un máximo y un mínimo absoluto en algunos puntos de $D$.

Para hallar los valores máximos y mínimos absolutos, es suficiente con encontrar los valores máximos y mínimos correspondientes a los puntos críticos y luego hallar los valores correspondientes a los puntos sobre la frontera $D$, el mayor será el máximo absoluto y el menor será el mínimo absoluto.

7. Multiplicadores de Lagrange

Los multiplicadores de Lagrange es una técnica que permite encontrar el máximo y mínimo de una función $f(x,y,z)$ limitada por otra $g(x,y,z)=k$ para ello se debe resolver el sistema de ecuaciones:

$\nabla f(x,y,z)=\lambda \nabla g(x,y,z)$

$g(x,y,z)=k$

En este caso $k$ es el valor de la superficie que limita la función $f$

Una extensión de este método usando dos restricciones implica que el sistema de ecuaciones simultaneas sea:

$\nabla f(x,y,z)=\lambda \nabla g(x,y,z) + \mu \nabla h(x,y,x)$

$g(x,y,z)=k$

$h(x,y,z)=c$

8. Artículos de Interés

Funciones de dos variables y Superficies

Límites en Cálculo

Derivadas en Cálculo

Las Funciones Vectoriales se utilizan frecuentemente en el estudio de fenómenos físicos y son de suma importancia como punto de entrada a conceptos más avanzados en cálculo y otras disciplinas de las matemáticas. Aquí se introducen las principales características y conceptos relacionados.

Si quieres aprender cálculo este es un buen lugar para iniciar.

1. Introducción a Funciones Vectoriales

Una función vectorial es similar a una función de una variable, simplemente que en lugar definirse como una regla que asigna valores numéricos correspondientes a valores de una variable, asigna vectores a valores correspondientes de una variable comúnmente llamada parámetro y simbolizado por $t$

Una función vectorial se puede definir de la siguiente manera:

$\textbf r(t)=f(t) \textbf i+g(t) \textbf j+h(t) \textbf k$

Las ecuaciones siguientes se conocen como ecuaciones paramétricas de la función:

$x=f(t), y=g(t), z=h(t)$

El límite de la función lo podemos escribir como:

$\lim_{t \to a}{\textbf r(t)}=\lim_{t \to a}{f(t)} \textbf i + \lim_{t \to a}{g(t)} \textbf j + \lim_{t \to a}{h(t)} \textbf k$

En este sentido la continuidad de la función se define de forma similar al caso de funciones ordinarias, la función es continua entonces si el limite de la función en un valor dado $a$ es igual al valor de la función en ese punto.

$\lim_{t \to a}\textbf r(a)=\textbf r(a)$

2. Derivadas e Integrales de Funciones Vectoriales

Las derivadas e integrales de las funciones vectoriales se definen de forma similar al caso en que las funciones sean ordinarias.

2.1. Derivadas de Funciones Vectoriales

La derivada de la función vectorial se define como:

$\textbf r'(t)=f'(t) \textbf i+g'(t) \textbf j+h'(t) \textbf k$

Las reglas de derivación y la interpretación de segundas derivadas conserva la misma interpretación que en el caso de funciones ordinarias.

Sean dos funciones vectoriales $\textbf u(t)$ y $\textbf v(t)$ y $f(t) una función ordinaria entonces:

• $\frac{d}{dt}[\textbf u+\textbf v]=\textbf u’ + \textbf v’$
• $\frac{d}{dt}[c\textbf u]=c\textbf u’$
• $\frac{d}{dt}[f \textbf u]=f’\textbf u + f \textbf u’$
• $\frac{d}{dt}[\textbf u \cdot \textbf v]=\textbf u’ \cdot \textbf v + \textbf u \cdot \textbf v’$
• $\frac{d}{dt}[\textbf u \times \textbf v]=\textbf u’ \times\textbf v + \textbf u \times\textbf v’$
• $\frac{d}{dt}[\textbf u(f(t))]=f’\textbf u(t)'(f(t))$

Esta última es la conocida como regla de la cadena en el caso vectorial.

2.2. Integrales de Funciones Vectoriales

Para el caso de las integrales, se utiliza la definición de integrales de funciones ordinarias de la siguiente forma:

$\int_a^b{\textbf r(t)dt}=\int_a^b{f(t)dt}\textbf i+\int_a^b{g(t)dt}\textbf j+\int_a^b{h(t)dt}\textbf k$

3. Longitud de arco y curvatura

La longitud de arco de una curva dada por una función vectorial, entre los parámetros $a$ y $b$ en un espacio $\mathbf R^3$ se puede definir como:

$L=\int_a^b{|\textbf r'(t)|dt}$

En general, una misma curva $C$ puede expresarse con diferentes funciones vectoriales, con lo cual cada una de las funciones que representan la curva $C$ se denominan parametrizaciones de la curva.

Una parametrización que a menudo resulta útil (porque no depende de ningún sistema coordenado) es la parametrización usando la longitud de arco.

Sea la longitud de arco:

$\frac{ds}{dt}=|\textbf r'(t)|$

Se puede parametrizar realizando la sustitución:

$t:\textbf r=\textbf r(t(s))$

3.1. Curvatura

La curvatura de una curva, en un punto ddo se define como se define como:

$\kappa(t)=|\frac{d\textbf T}{ds}|=\frac{|\textbf r'(t) \times \textbf r”(t)|}{|\textbf r’)t)|^3}$

Siendo $\\textbf T(t)$ el vector tangente unitario dado por:

$\textbf T(t)=\frac{\textbf r'(t)}{|\textbf r'(t)|}$

Dado el vector anterior, también es posible definir en un punto dado de la curva ecuaciones para el vector normal unitario principal $\textbf N(t)$ y el vector binormal $\textbf B(t)$ dados por las siguientes ecuaciones:

$\textbf N(t)=\frac{\textbf T'(t)}{|\textbf T'(t)|}$

$\textbf B(t)=\textbf T(t) \times \textbf N(t)$

4. Superficies paramétricas

Las funciones vectoriales en función de un único parametro describen curvas en $\mathbb R^3$, similarmente las funciones vectoriales de dos parametros pueden describir superficies en $\mathbb R^3$, en este caso la ecuación de esta superficie esta dada por:

$\textbf r(u,v)=x(u,v)\textbf i + y(u,v)\textbf j + z(u,v)\textbf k$

5. Artículos de Interés

Derivadas en Cálculo

Integrales en Cálculo

Series en Matemáticas y Cálculo

Las series de potencias son una herramienta tremendamente útil en Cálculo y permiten representar una función como una sumatoria, en este artículo se recopila los principales resultados de las Series de Potencias de Taylor y Maclaurin en Cálculo.

Si quiere aprender sobre lo básico de series siga este enlace.

1. Series de potencias

La Serie de Potencias en Cálculo es aquella que viene dada por la forma:

$\sum_{x=0}^{\infty}c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+\dots$

Donde $x$ es una variable y las $c_n$ son constantes llamadas coeficientes de la serie. Note que una serie corresponde a un polinomio de grado infinito. De forma más general se puede escribir la serie como:

$\sum_{x=0}^{\infty}c_n(x-a)^n=c_0+c_1(x-a)+c_2(x-a)^2+c_3(x-a)^3+\dots$

La cual se denomina serie de potencias en $x-a$ o serie de potencias centrada en $a$

En general para una serie de potencias $\sum_{x=0}^{\infty}c_n(x-a)^n$ centrada en $a$ sólo existen tres posibilidades:

• La serie converge solo cuando $x=a$
• La serie converge para toda $x$
• Hay un número positivo $R$, tal que la serie converge si $|x-a| \lt R$ y diverge si $|x-a|>R$

El número $R$ es conocido como radio de convergencia de la serie de potencias y dependiendo de alguno de los tres casos anteriores, todos los valores de xx para los cuales la serie converge se conocen como intervalo de convergencia.
Hay que tener en cuenta que para la mayoría de las series de potencias se puede utilizar la prueba de la razón para obtener un criterio de convergencia y el intervalo de convergencia, sin embargo, para los extremos del intervalo esta prueba no es aplicable y debe sustituirse el valor del intervalo en la serie y determinar por algún otro medio la convergencia de la misma en estos puntos.

2. Representación de funciones como series de potencias

Las funciones matemáticas pueden representarse usando una serie de potencias, y para ello es importante retomar la serie:

$\frac{1}{1-x}=1+x+x^2+x^2+x^3+\dots=\sum_{n=0}^{\infty}x^n\text{ }|x|<1$

De esta forma también podemos escribir:

$f(x)=\frac{1}{1-x}=\sum_{n=0}^{\infty}x^n\text{ }|x|<1$

Tenga presente que se pueden transformar las funciones usando álgebra básica para representarlas como series de potencias y que no todas las funciones se pueden representar como una serie de potencias.

3. Derivación e integración de las series de potencias

La suma de una serie de potencias de una función, permite obtener la derivada y la integral de dicha función derivando termino a termino. Si la serie de potencias $\sum c_n(x-a)^n$ tiene el radio de convergencia $R>0$, entonces la función $f$ definida por

$f(x) =c_0+c_1(x-a)+c_2(x-a)^2+\dots=\sum_{n=0}^{\infty}c_n(x-a)^n$

es derivable y como consecuencia continua en el intervalo $(a-R,a+R)$ y

• $f'(x) =c_1+2c_2(x-a)+3c_3(x-a)^2+\dots=\sum_{n=1}^{\infty}nc_n(x-a)^{n-1}$
• $\int f(x)dx =C+c_0(x-a)+c_1\frac{(x-a)^2}{2}+c_2\frac{(x-a)^3}{3}+\dots=C+\sum_{n=0}^{\infty}c_n\frac{(x-a)^{n+1}}{n+1}$

Los radios de convergencia de las series de potencias anteriores son $R$. Las ecuaciones anteriores pueden volver a escribirse de la siguiente manera:

• $\frac{d}{dx}\left[\sum_{n=0}^{\infty} c_n(x-a)^n \right] = \sum_{n=0}^{\infty} \frac{d}{dx} [c_n(x-a)^n]$
• $\int\left[\sum_{n=0}^{\infty} c_n(x-a)^n \right] = \sum_{n=0}^{\infty} \int [c_n(x-a)^n]$

Estas ecuaciones afirman que la derivada de una suma es la suma de las derivadas y la integral de una suma es la suma de las integrales incluso para sumas infinitas. Debe tenerse mucho cuidado puesto que lo anterior solo es cierto para sumas de series de potencias y no para otro caso. Los resultados expuestos aquí son muy útiles, puesto que permiten expresar una función como una serie incluso para funciones menos usuales a través del uso de sus derivadas y sus integrales conocidas.

4. Series de Taylor y Maclaurin

Dado que una función se puede representar como serie de potencias, usando derivadas y teniendo presente que en $x=a$ los términos que contienen $x$ se anulan se puede escribir los coeficientes de la serie de potencias en términos de $f$ así:

Si $f$ tiene una representación en series de potencias centradas en $a$, esto es:

$f(x)=\sum_{n=0}^{\infty}c_n(x-a)^n\text{ cuando } |x-a| \lt R$

entonces los coeficientes de la serie pueden ser expresados por la fórmula:

$c_n=\frac{f^{(n)}(a)}{n!}$

La serie resultante tiene dos casos:

1. Serie de potencias centrada en $0$, conocida como serie de Maclaurin

$f(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n$

2. Serie de potencias centrada en $a$, conocida como serie de Taylor

$f(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n$

4.2 Teoremas y definiciones

Las representaciones de las series de Taylor y Maclaurin pueden coincidir con la función y para demostrar ello los siguiente resultados son útiles.

Definición: Polinomio de Taylor Las sumas parciales de la serie de Taylor equivalen a un polinomio de grado $n$ que se puede expresar como:

$T_n(x)=\sum_{i=0}^{\infty}\frac{f^{(i)}(a)}{i!}(x-a)^i$

Definición: Residuo de la serie de Taylor Se define el residuo de la serie de Taylor como el polinomio de grado $n$ entre el polinomio de Taylor de grado $n$ y la función $f$, así:

$R_n(x)=f(x)-T_n(x)$

Note que si $\lim_{n \to \infty}R_n(x) = 0$ entonces la serie de Taylor y la función coinciden.

Teorema Si $f(x)=T_n(x)+R_n(x)$, donde $T_n(x)$ es el polinomio de Taylor y $R_n(x)$ es el residuo de la serie de Taylor de n-esimo grado de $f$ en $a$ y si

$\lim_{n \to \infty}R_n(x)=0$

para $|x-a| \lt R$, entonces $f$ es igual a la suma de su serie de Taylor en el intervalo $|x-a| \lt R$

Teorema Desigualdad de Taylor El siguiente resultado es útil para demostrar que el residuo de la serie de Taylor es cero.
Si $|f^{(n+a)}(x)|\le M$ para $|x-a| \le d$, entonces el residuo $R_n(x)$ de la serie de Taylor satisface la desigualdad:

$|R_n(x)| \le \frac{M}{(n+1)!}|x-a|^{n+1} \text{ para } |x-a| \le d$

4.3. Resultados importantes

Algunos de los resultados más importantes que tienen relación con las series de Taylor y Maclaurin de funciones conocidas se recopilan a continuación:

• $\lim_{n \to \infty}\frac{x^n}{n!}=0 \text{ para todo número real x}$
• $\frac{1}{1-x}=\sum_{n=0}^{\infty}x^n \text{ para todo número real x entre (-1,1)}$
• $e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}\ text{ para todo número real x}$
• $\sin x=\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n+1}}{(2n+1)!} \text{ para todo número real x}$
• $\cos x=\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n}}{(2n)!} \text{ para todo número real x}$
• $\arctan x=\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n+1}}{2n+1} \text{ para todo número real x entre [-1,1]}$

5. Artículos de Interés

Derivadas en Cálculo

Integrales en Cálculo

Determinantes en Álgebra Lineal

Las series y sucesiones son un tema muy importante en matemáticas de hecho permiten representar de una forma diferente funciones o números, en este artículo encontraras todo lo concerniente a Teoremas y Pruebas de Series en Cálculo a fin de poder determinar si las mismas convergen o divergen.

Si quieres aprender lo básico de series y sucesiones sigue este link.

1. Prueba de la convergencia

El primer Teorema de Series en Cálculo es el de la convergencia. Si la serie $\sum_{n=1}^{\infty}{a_n}$ es convergente, entonces $\lim_{n\to\infty}{a_n}=0$
Nota: el inverso de este teorema por lo regular es falso. Hay que diferenciar en este punto del límite de las sumas parciales al límite de los términos, ambos son límites que se le pueden asociar a cualquier serie.

2. Prueba de la divergencia

Esta es la prueba que ayuda a determinar si una Serie en Cálculo converge y establece que Si $\lim_{n\to\infty}{a_n}$ no existe, o si $\lim_{n\to\infty}{a_n} \ne 0$, entonces la serie $\sum_{n=1}^{\infty}{a_n}$ diverge

3. Convergencia de series

Si `\sum{a_n}` y `\sum{b_n}` son series convergentes, entonces también lo son las series: `\sum{ca_n}` (donde `c` es una constante), `\sum{(a_n+b_n)}`, `\sum{a_n-b_n}` y

• $\sum_{n=1}^{\infty}{ca_n}=c\sum_{n=1}^{\infty}{a_n}$
• $\sum_{n=1}^{\infty}{(a_n+b_n)}=\sum_{n=1}^{\infty}{a_n}+\sum_{n=1}^{\infty}{b_n}$
• $\sum_{n=1}^{\infty}{(a_n-b_n)}=\sum_{n=1}^{\infty}{a_n}-\sum_{n=1}^{\infty}{b_n}$

4. Prueba de la integral

Suponga que $f$ es una función continua, positiva y decreciente en $[1,\infty)$ y sea $a_n=f(n)$. Entonces la serie $\sum_{n=1}^\infty a_n$ es convergente si y sólo si la integral impropia $\int_1^\infty f(x)dx$ es convergente. En resumen:

• Si $\int_1^\infty f(x)dx$ es convergente, entonces $\sum_{n=1}^\infty a_n$ es convergente.
• Si $\int_1^\infty f(x)dx$ es divergente, entonces $\sum_{n=1}^\infty a_n$ es divergente.

Un resultado importante al aplicar la prueba de la integral es el siguiente:

Si la serie $p$, $\sum_{n=1}^\infty \frac{1}{n^p}$ es convergente si $p>1$ y diverge cuando $p \le 1$.

5. Prueba de la comparación

Suponga que $\sum a_n$ y $\sum b_n$ son series con términos positivos.

• Si $\sum bn$ es convergente y $a_n \le b_n$ para toda $n$, entonces $\sum a_n$ también converge.
• Si $\sum bn$ es divergente y $a_n \ge b_n$ para toda $n$, entonces $\sum a_n$ también diverge.

6. Prueba de comparación de límites

Suponga que $\sum a_n$ y $\sum b_n$ son series con términos positivos. Si

$\lim_{n \to \infty}\frac{a_n}{b_n}=c$

Donde $c$ es un número finito y $c>0$, entonces ambas series convergen o divergen.

7. Estimado del residuo para la prueba de la integral

Suponga que $f(x)=a_k$, donde $f$ es una función decreciente, continua y positiva para $x \ge n$ y $\sum a_n$, converge. Si $R_n=s-s_n$, entonces:

$\int_{n+1}^{\infty}f(x)dx \le R_n \le \int_{n}^{\infty}f(x)dx$

De donde se obtiene inmediatamente:

$s_n+\int_{n+1}^{\infty}f(x)dx \le s \le s_n+\int_{n}^{\infty}f(x)dx$

8. Prueba de la serie alternante

Si la serie alternante

$\sum_{n=1}^\infty{(-1)^{n-1}b_n}\text{ con }(b_n>0)$

Satisface:

• $b_{n+1} \le b_n$
• $\lim_{n\to \infty}b_n=0$

Entonces la serie converge.

9. Teorema de estimación de la serie alternante

Si $s=\sum(-1)^{n-1}b_n$ es la suma de una serie alternante que satisface:

• $b_{n+1} \le b_n$
• $\lim_{n\to \infty}b_n=0$

Entonces:

$|R_n|=|s-s_n| \le b_n+1$

10. Convergencia absoluta

La serie $\sum a_n$ es absolutamente convergente si la serie de valores absolutos $\sum |a_n|$ converge.
Si una serie $\sum a_n$ es absolutamente convergente, entonces es convergente.

11. Prueba de la razón

Si $\lim_{n \to \infty} |\frac{a_{n-1}}{a_n}|=L<1$, entonces la serie $\sum_{n=1}^\infty{a_n}$ es absolutamente convergente y, por lo tanto, convergente.

Si $\lim_{n \to \infty} |\frac{a_{n-1}}{a_n}|=L>1$ o $\lim_{n \to \infty}|\frac{a_{n-1}}{a_n}|=\infty$ entonces la serie $\sum_{n=1}^\infty{a_n}$ es divergente.

Si $\lim_{n \to \infty} |\frac{a_{n-1}}{a_n}|=L=1$, entonces la prueba de la razón no es concluyente.

12. Artículos de Interés

Derivadas en Cálculo

Integrales en Cálculo

Geometría Vectorial

A continuación se presentan una serie de Técnicas de Integración en Cálculo que permiten realizar el proceso de integración, de integrales complejas que no se encuentran relacionadas en las integraciones de funciones básicas definidas al principio de esta página.

Si quieres aprende sobre derivación sigue el siguiente link.

1. Sustitución

La regla de sustitución es muy versátil y aplica en muchos casos, esta regla es correspondiente a la regla de la cadena para la derivación y establece de forma general lo siguiente: Si $u=g(x)$ es una función derivable cuyo rango es un intervalo $I$ y $f$ es continua sobre $I$, entonces:

$\int f(g(x))g'(x)dx=\int f(u)du$

La regla de la sustitución también funciona para la evaluación de integrales definidas, en este caso la regla establece lo siguiente:

$\int_a^b f(g(x))g'(x)dx=\int_{g(a)}^{g(b)} f(u)du=F(g(x))\biggr\rvert_a^b=F(u)\biggr\rvert_{g(a)}^{g(b)}$

Un ejemplo de la aplicación de esta regla se da a continuación:

Integrar $\int x^3\cos (x^4+2)dx$, para este caso hagamos $u=x^4+2$, de tal forma que $du=4x^3dx$ o lo que es lo mismo $x^3dx=\frac{du}{4}$, la integral original queda de la forma: $\int \frac{\cos(u)}{4}du=\sin(u)$, finalmente reemplazamos de nuevo para volver a la variable original $x$ de esta manera la respuesta a la integral es: $\sin(x^4+2)$ lo cual se puede corroborar mediante derivación.

2. Simetría

Se puede aplicar simetría para evaluar funciones definidas si estas son pares o impares de la siguiente manera:

• Si una función es par f(x)=f(−x)f(x)=f(-x) entonces la integral ∫a−af(x)dx=2∫a0f(x)dx∫-aaf(x)dx=2∫0af(x)dx
• Si una función es par $f(x)=f(-x)$ entonces la integral $\int_{-a}^af(x)dx=2\int_0^af(x)dx$
• Si una función es impar $f(-x)=-f(x)$ entonces la integral $\int_{-a}^af(x)dx=0$

3. Integración por partes

Entre las Técnicas de Integración en Cálculo, la integración por partes hace uso de la regla del producto para derivación a fin de simplificar la integral y obtener una integral más sencilla. En términos generales se puede escribir la regla de integración por partes de la siguiente manera:

$\int udv = uv-\int vdu$

Se debe elegir en la integral original $u$ y $v$ de manera que $u$ sea fácil de derivar y sea fácil obtener $v$ integrando $dv$.

A continuación se muestra un ejemplo de aplicación de esta regla. Integrar

$\int e^x\sin x dx$ 

Elegimos:

$u=e^x$ de forma que $du=e^xdx$

$dv=sinxdx$ de forma que $v=−cosx$

Reemplazando en la fórmula de integración por partes se obtiene:

$\int e^x\sin x dx=-e^x\cos x-\int (-\cos x)e^xdx$

En este caso debemos volver a integrar por partes pues la segunda integral es igual de compleja que la original. En este nuevo caso tenemos que resolver la integral 

\int e^x\cos xdx

Elegimos:

$u=e^x$ de forma que $du=e^xdx$
$dv=\cos xdx$ de forma que $v=\sin x$

Reemplazando en la fórmula de integración por partes se obtiene:

$\int e^x\cos xdx=e^x\sin x – \int e^x\sin xdx$

Ahora se reemplaza este resultado en la primera integral por partes obteniendo:

$\int e^x\sin x dx=-e^x\cos x + e^x\sin x – \int e^x\sin xdx$

Para finalmente despejar y obtener la solución:

$\int e^x\sin x dx=\frac{-e^x\cos x + e^x\sin x}{2}$

4. Integración trigonométrica

Otra Técnica de Integración en Cálculo es la sustitución trigonométrica la cual es útil cuando se tiene integrales que impliquen raíces. Las siguientes sustituciones pueden ser útiles:

• Un factor de la forma $\sqrt{a^2-x^2}$ puede tratarse con la sustitución $x=a\sin \theta$
• Un factor de la forma $\sqrt{a^2+x^2}$ puede tratarse con la sustitución $x=a\tan \theta$
• Un factor de la forma $\sqrt{x^2-a^2}$ puede tratarse con la sustitución $x=a\sec \theta$

A continuación se muestra un ejemplo del uso de esta técnica. Integrar

$\int \sqrt{r^2-x^2}dx$

Usamos la sustitución: $x=r\sin\theta$ lo que equivale a $\theta=\sin^{-1}\frac{x}{r}$ Y por lo tanto $dx=r\cos\theta d\theta$ La integral original es ahora:

$\int \sqrt{r^2-x^2}dx=r\int \sqrt{r^2-r^2\sin^2\theta}\cos\theta d\theta=r\int\sqrt{r^2\cos^2\theta}\cos\theta d\theta=r^2\int\cos^2\theta d\theta$

Para resolver esta nueva integral recurrimos a las fórmulas de ángulo doble:

$\cos^2\theta=\frac{1}{2}(1+\cos{2\theta})$

Convirtiendo nuevamente esta integral trigonométrica en:

$r^2\int\cos^2\theta d\theta=r^2\int \frac{1}{2}(1+\cos{2\theta})d\theta=r^2\biggl(\frac{\theta}{2}+\frac{\sin{2\theta}}{4}\biggl)$

Al volver a la variable original se obtiene:

$\int \sqrt{r^2-x^2}dx=r^2\biggl(\frac{\sin^{-1}\frac{x}{r}}{2}+\frac{\sin{(2\sin^{-1}\frac{x}{r}})}{4}\biggl)$

5. Integración por fracciones parciales

La técnica de fracciones parciales permite reducir una fracción dada en forma de cociente de polinomios a una forma más sencilla en términos de fracciones simples que pueden integrarse fácilmente. Por ejemplo la integral:

$\int \frac{5x-4}{2x^2+x-1}dx$

Puede simplificarse notablemente si se aplica fracciones parciales:

$\int \biggl( \frac{3}{x+1}-\frac{1}{2x-1} \biggr)dx$

Esta última integral es muy fácil de resolver aplicando sustituciones.

6. Artículos de Interés

Aplicaciones Prácticas de la Derivación

Límites en Cálculo

Integrales en Cálculo

Cuando estudiamos derivadas y cualquier rama de la matemática queremos encontrar en que situaciones reales o aplicadas las podemos utilizar, en este artículo se explora los resultados más útiles de Aplicaciones Practicas de la Derivación.

Si quieres aprender Álgebra Lineal te recomiendo seguir este enlace.

1. Máximos y mínimos

Una función $f$ tiene un máximo absoluto (o máximo global) en $c$ si $f(c) \ge f(x) \forall x \in D$, donde $D$ es el dominio de $f$. El número $f(c)$ se llama valor máximo de $f$ en $D$, De manera análoga, $f$ tiene un mínimo absoluto en $c$ si $f(c) \le f(x) \forall x \in D$; el número $f(c)$ se denomina valor mínimo de $f$ en $D$, los valores máximo y mínimo de $f$ se conocen como valores extremos de $f$, Una función $f$ posee un máximo local (o máximo relativo) en $c$ si $f(c) \ge f(x)$ cuando $x$ está cercano a $c$ o alternativamente para todo $x$ en un intervalo abierto que contiene a $c$, De manera análoga, $f$ tiene un mínimo local en $c$ si $f(c) \le f(x)$ cuando $x$ está cerca de $c$.

2. Teorema del valor extremo

Una de las Aplicaciones Prácticas de la Derivación es el Teorema del Valor Extremo que se analiza aquí. Si $f$ es continua sobre un intervalo cerrado $[a,b]$, entonces $f$ alcanza un valor máximo absoluto $f(c)$ y un valor mínimo absoluto $f(d)$ en algunos números $c$ y $d$ en $[a,b]$

3. Teorema de Fermat

Si $f$ tiene un máximo o un mínimo locales en $c$ y si $f'(c)$ existe, entonces $f'(c)=0$.
Es importante anotar respecto de este teorema que dice que los máximos o mínimos cumplen una condición y no que en los puntos en los cuales $f'(c)=0$ sea necesariamente un máximo o un mínimo; en otras palabras el teorema de Fermat da los puntos en los cuales se podría comenzar a buscar máximos y mínimos.

4. Números críticos

Un número críticos son otra de las Aplicaciones Prácticas de la Derivación y para una función $f$ es un número $c$ en el dominio de $f$ tal que $f'(c)=0$ o $f'(c)$ no existe. Con esta definición se podría reescribir el teorema de Fermat de la siguiente manera: Si $f$ tiene un extremo local en $c$, entonces $c$ es un número crítico de $f$.

5. Método del intervalo cerrado

El siguiente método permite hallar los máximos y mínimos absolutos de una función continua sobre un intervalo cerrado: Para hallar los valores máximos y mínimos absolutos de una función $f$ sobre un intervalo cerrado $[a,b]$:

• Encuentre los valores de $f$ en los números críticos de $f$ en $(a,b)$
• Halle los valores de $f$ en los puntos extremos del intervalo
• El más grande de los valores de los pasos anteriores es el valor máximo absoluto, el valor más pequeño es el valor mínimo absoluto.

6. Teorema del valor medio

Si es una función derivable sobre el intervalo $[a,b]$ entonces existe un número $c$ entre $a$ y $b$ tal que:

$f'(c)=\frac{f(b)-f(a)}{b-a}$

o lo que equivale a:

$f(b)-f(a)=f'(c)(b-a)$

En palabras lo que este teorema dice es entre el punto $a$ y $b$ se puede trazar una recta cuya pendiente es igual a la pendiente de la recta tangente en algún punto del recorrido que la función $f$ realiza de $a$ a $b$.

7. Prueba de la primera derivada

Esta prueba permite determinar los máximos y mínimos locales de una función. La prueba afirma lo siguiente: Suponga que $c$ es un número crítico de una función continua $f$

• Si $f’$ cambia de positiva a negativa en $c$ entonces $f$ tiene un máximo local en $c$
• Si $f’$ cambia de negativa a positiva en $c$ entonces $f$ tiene un mínimo local en $c$
• Si $f’$ no cambia de signo en $c$ entonces $f$ no tiene ni máximos ni mínimos locales en $c$

8. Prueba de la segunda derivada

Esta prueba permite determinar los máximos y mínimos locales de una función. La prueba afirma lo siguiente: Suponga que $f′′$ es continua cerca de $c$

• Si $f'(c)=0$ y $f”(c) \gt 0$ entonces $f$ tiene un mínimo local en $c$
• Si $f'(c)=0$ y $f”(c) \lt 0$ entonces $f$ tiene un máximo local en $c$

9. Artículos de Interés

Límites en Cálculo

Derivadas en Cálculo

Reglas de Derivación en Cálculo