Las Integrales Dobles y Triples son la aplicación del concepto de Integral al cálculo de múltiples variables, estas integrales aparecen frecuentemente en muchos campos como probabilidad, centros de masa, cálculo de volúmenes y un sin fin de aplicaciones a física y otras ramas del conocimiento.
Si quieres aprende sobre integrales puedes comenzar aquí.
1. Definición de integral doble
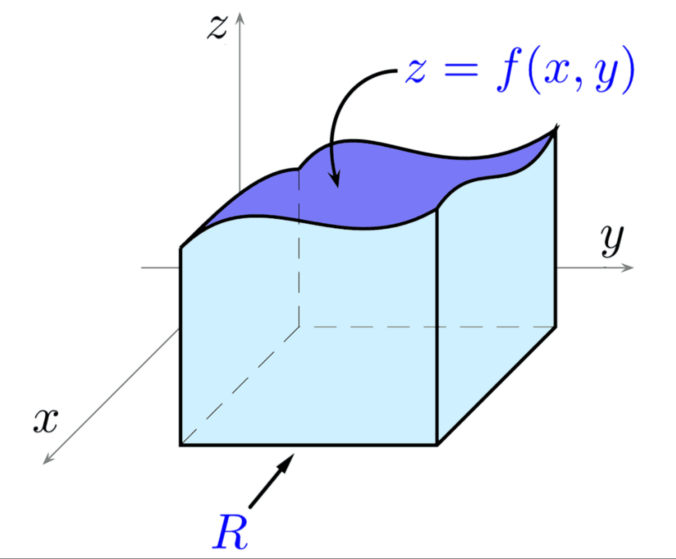
Esta definición de integral doble es bastante fácil de entender pues es simplemente la extensión a varias variables de la integral sencilla. Aquí es conveniente recordar que la integral de una variable es el área de la curva formada por la suma de rectangulos y haciendo que el ancho de estos rectangulos tienda a cero, similarmente con dos variables sería el volumen bajo la superficie determinado por:
$\iint_R{f(x,y)dA}=\lim_{m,n\to\infty}\sum_{i=1}^m{\sum_{j=1}^n}f(x_i,y_i)\delta A$
A la parte derecha de la ecuación anterior se le conoce como la Suma de Riemann. Si la función es positiva $f(x,y)>0$ se puede interpretar la integral como el volumen:
$V=\iint_R{f(x,y)dA}$
Similar al caso de una variable podemos encontrar el valor promedio de una función de dos variables usando:
$f_{prom}=\frac{1}{A(R)}\iint_R{f(x,y)dA}$
2. Propiedades de la Integrales dobles
Las integrales múltiples cumplen las mismas propiedades de las integrales simples:
- $\iint[f(x,y)+g(x,y)]dA=\iint f(x,y)dA+\iint g(x,y)dA$
- $\iint cf(x,y)dA=c\iint f(x,y)dA$
- Si $f(x,y) \ge g(x,y)$ entonces $\iint f(x,y)dA \ge \iint g(x,y)dA$
- Si $m \le f(x,y) \le M$ se cumple en el dominio de integracion $D$ entonces $mA(D) \le \iint_D{f(x,y)dA} \le MA(D)$
3. Integrales iteradas y Teorema de Fubini
Para calcular integrales dobles se puede realizar el cálculo de una de las integrales primero que la otra de forma iterada, elegir cual variable se integra primero conduce a que sea más fácil calcular la segunda. El Teorema de Fubini establece que el orden en que se calculan las derivadas produce el mismo resultado.
Sea $f$ continua en $R={(x,y)|a \le x\le b, c \le y \le d}$ entonces
$\iint_R{f(x,y)dA}=\int_a^b\int_c^d{f(x,y)dydx}=\int_c^d\int_a^b{f(x,y)dxdy}$
Una consecuencia del Teorema de Fubini que puede simplificar el cálculo de algunas integrales es si la función se puede dividir como dos funciones exclusivamente de $x$ y $y$:
$\iint_R{g(x)h(y)dA}=\int_a^b{g(x)dx}\int_c^d{h(y)dy}$
4. Integrales dobles sobre regiones generales
En las integrales definidas anteriormente, la región de integración corresponde a un rectangulo sobre el plano $XY$, sin embargo se puede realizar integrales sobre regiones más generales definidas por curvas dependintes de $x$ (regiones tipo I) o curvas dependientes de $y$ (regiones tipo II).
A continuación se muestran las ecuaciones para calcular estas integrales.
Para regiones tipo I:
$D={(x,y) \in a \le x \le b, g_1(x) \le y \le g_2(x)}$
$\int_D{f(x,y)dA}=\int_a^b\int_{g_1(x)}^{g_2(x)}{f(x,y)dydx}$
Para regiones tipo II:
$D={(x,y) \in c \le y \le d, h_1(x) \le x \le h_2(x)}$
$\int_D{f(x,y)dA}=\int_c^d\int_{h_1(x)}^{h_2(x)}{f(x,y)dxdy}$
También es importante notar que una región más general se puede partir y obtener la integral como la suma de las integrales así:
Si $D = D_1 \cup D_2$ entonces:
$\iint_D{f(x,y)dA}=\iint_{D_1}{f(x,y)dA}+\iint_{D_2}{f(x,y)dA}$
4.1. Integrales dobles en coordenadas polares
Para realizar una integral en coordenadas polares puede utilizarse el siguiente cambio de variable:
Si $f$ es continua en un rectangulo polar dado por $R$ tal que $0 \le a \le r \le b$ y $\alpha \le \theta \le \beta$ y $0 \le \beta – \alpha \le 2 \pi$ entonces:
$\iint_R{f(x,y)dA}=\int_\alpha^\beta\int_a^b{f(r\cos\theta,r\sin\theta)rdrd\theta}$
Note que también puede integrar sobre funciones que definan los arcos similar al caso de integrales sobre regiones generales en coordenadas rectangulares.
5. Aplicaciones de Integrales dobles
Algunas de las aplicaciones más comunes de integrales dobles se muestran a continuación, estas aplicaciones fácilmente pueden ser extendidas a más de dos dimensiones utilizando integrales triples.
5.1. Masa
Dada la densidad, que es la masa por unidad de área y si esta densidad es variable se puede utilizar esta definición para calcular la masa usando:
$m=\iint_D{\rho(x,y)dA}$
5.2. Momentos
Los momentos de masa se pueden entender desde su aplicación que permite obtener el centro de masa de una lámina, estos centros de masa equivalen al punto donde la lámina se equilibra y es equivalente a tener toda la mas ubicada en ese punto, a continuación se dan las ecuaciones de los momentos y centros de masa de una lámina con densidad variable.
$M_x=\iint_D{y\rho(x,y)dA}$
$M_y=\iint_D{x\rho(x,y)dA}$
Y el centro de masa:
$\bar x=\frac{1}{m}\iint_D{x\rho(x,y)dA}$
$\bar y=\frac{1}{m}\iint_D{y\rho(x,y)dA}$
Los segundos momentos son conocidos así pues representan el momento de inercia de la lámina, a continuación se muestran estos momentos respecto a los ejes y al origen, este último también se conoce como momento polar de inercia:
$I_x=\iint_D{y^2\rho(x,y)dA}$
$I_y=\iint_D{x^2\rho(x,y)dA}$
$I_0=\iint_D{(x^2+y^2)\rho(x,y)dA}$
5.2. Área Superficial
El área de una superficie se puede calcular con el uso de integrales dobles, si tenemos la representación paramétrica de la superficie:
$\mathbf r=x(u,v)\mathbf i + y(u,v) \mathbf j + z(u,v) \mathbf k$
Entonces el área superficial esta definida por:
$A(S)=\iint_D{1\mathbf r_u \times \mathbf r_v| dA}$
Donde
$\mathbf r_u=\frac{\partial x}{\partial u}\mathbf i + \frac{\partial y}{\partial u} \mathbf j + \frac{\partial z}{\partial u} \mathbf k$
$\mathbf r_v=\frac{\partial x}{\partial v}\mathbf i + \frac{\partial y}{\partial v} \mathbf j + \frac{\partial z}{\partial v} \mathbf k$
Alternativamente se puede calcular como:
$A(S)=\iint_D{\sqrt{1+\frac{\partial z}{\partial x}^2+\frac{\partial z}{\partial y}^2}dA}$
6. Integrales triples
Las integrales triples son muy parecidas a las integrales dobles excepto que existe una variable adicional, además aplican las mismas reglas y principios. En este caso no existe una interpretación gráfica como tal ya que la región de integración es un volumen y se esta integrando una función de tres variables cuyos valores se requerirían dibujar en el hiperespacio cuadridimensional.
El teorema de Fubini aplica de igual manera y las regiones de integración no necesariamente deben ser cubos, sino que pueden ser funciones que acoten la región.
En general la integral de tres variables se define con sumas de Reimann y se puede escribir como:
$\iiint_B{f(x,y,z)dV}=\int_r^s\int_c^d\int_a^b{f(x,y,z)dxdydz}$
Para regiones generales se puede establecer integrales como la siguiente:
$\iiint_B{f(x,y,z)dV}=\int_a^b\int_{g_1(x)}^{g_2(x)}\int_{u_1(x,y)}^{u_2(x,y)}{f(x,y,z)dxdydz}$
6.1. Integrales triples en coordenadas cilíndricas
El cambio de variable para coordenadas cilíndricas en integrales triples arroja el siguiente resultado:
$\iiint_B{f(x,y,z)dV}=\int_\alpha^\beta\int_{h_1(\theta)}^{h_2(\theta)}\int_{u_1(r\cos\theta,r\sin\theta)}^{u_2(r\cos\theta,r\sin\theta)}{f(r\cos\theta,r\sin\theta,z)rdzdrd\theta}$
6.2. Integrales triples en coordenadas esféricas
El cambio de variable para coordenadas esféricas en integrales triples arroja el siguiente resultado:
$\iiint_B{f(x,y,z)dV}=\int_c^d\int_\alpha^\beta\int_a^b{f(\rho\sin\phi\cos\theta,\rho\sin\phi\sin\theta,\rho\cos\phi)\rho^2\sin\phi d\rho d\theta d\phi}$
7. Cambio de variables y Jacobiano
La transformación o cambio de una variable cuando la integral es de una sola variable se puede realizar de la siguiente manera:
$\int_a^b{f(x)dx}=\int_c^d{f(g(u))g'(u)du}$
La equivalencia entre los límites esta dada por $x=g(u)$ es decir $a=g(c)$ y $b=g(d)$.
En el caso de dos o más variables, también se puede realizar cambios de variables, como el de coordenadas polares, cilíndricas o esféricas. Para realizar este cambio debemos comprender que se esta transformando la región original de integración en una nueva y que para ello denotamos el nuevo plano y los nuevos límites con nombres de variables diferentes. Así mismo, definimos que una transformación $T$ es una $transformacion C^{-1}$ lo cual indica que las funciones de transformación $g$ y $h$ tienen derivadas parciales continuas.
$x=g(u,v)$
$y=h(u,v)$
Las nuevas variables son $u$ y $v$ y el la región original $R$ se llamará ahora $S$.
En general integrar realizando un cambio de variables en dos o más variables es conveniente definir el siguiente determinante que se conoce como el jacobiano:
$\frac{\partial (x,y)}{\partial (u,v)}=\left| \begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial x}{\partial v} \end{array} \right|=\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial x}{\partial v}\frac{\partial y}{\partial u}$
Con esta definición el cambio de variables en dos variables se puede escribir como:
$\iint_R{f(x,y)dA}=\iint_S{f(x(u,v),y(u,v))|\frac{\partial (x,y)}{\partial (u,v)}|dudv}$

Deja un comentario
Lo siento, debes estar conectado para publicar un comentario.