Mes: diciembre 2023

Las Integrales Dobles y Triples son la aplicación del concepto de Integral al cálculo de múltiples variables, estas integrales aparecen frecuentemente en muchos campos como probabilidad, centros de masa, cálculo de volúmenes y un sin fin de aplicaciones a física y otras ramas del conocimiento.

Si quieres aprende sobre integrales puedes comenzar aquí.

1. Definición de integral doble

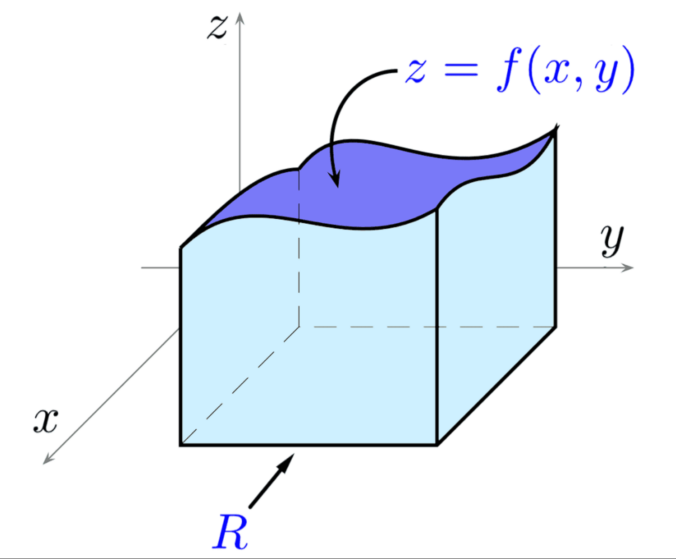
Esta definición de integral doble es bastante fácil de entender pues es simplemente la extensión a varias variables de la integral sencilla. Aquí es conveniente recordar que la integral de una variable es el área de la curva formada por la suma de rectangulos y haciendo que el ancho de estos rectangulos tienda a cero, similarmente con dos variables sería el volumen bajo la superficie determinado por:

$\iint_R{f(x,y)dA}=\lim_{m,n\to\infty}\sum_{i=1}^m{\sum_{j=1}^n}f(x_i,y_i)\delta A$

A la parte derecha de la ecuación anterior se le conoce como la Suma de Riemann. Si la función es positiva $f(x,y)>0$ se puede interpretar la integral como el volumen:

$V=\iint_R{f(x,y)dA}$

Similar al caso de una variable podemos encontrar el valor promedio de una función de dos variables usando:

$f_{prom}=\frac{1}{A(R)}\iint_R{f(x,y)dA}$

2. Propiedades de la Integrales dobles

Las integrales múltiples cumplen las mismas propiedades de las integrales simples:

• $\iint[f(x,y)+g(x,y)]dA=\iint f(x,y)dA+\iint g(x,y)dA$
• $\iint cf(x,y)dA=c\iint f(x,y)dA$
• Si $f(x,y) \ge g(x,y)$ entonces $\iint f(x,y)dA \ge \iint g(x,y)dA$
• Si $m \le f(x,y) \le M$ se cumple en el dominio de integracion $D$ entonces $mA(D) \le \iint_D{f(x,y)dA} \le MA(D)$

3. Integrales iteradas y Teorema de Fubini

Para calcular integrales dobles se puede realizar el cálculo de una de las integrales primero que la otra de forma iterada, elegir cual variable se integra primero conduce a que sea más fácil calcular la segunda. El Teorema de Fubini establece que el orden en que se calculan las derivadas produce el mismo resultado.

Sea $f$ continua en $R={(x,y)|a \le x\le b, c \le y \le d}$ entonces

$\iint_R{f(x,y)dA}=\int_a^b\int_c^d{f(x,y)dydx}=\int_c^d\int_a^b{f(x,y)dxdy}$

Una consecuencia del Teorema de Fubini que puede simplificar el cálculo de algunas integrales es si la función se puede dividir como dos funciones exclusivamente de $x$ y $y$:

$\iint_R{g(x)h(y)dA}=\int_a^b{g(x)dx}\int_c^d{h(y)dy}$

4. Integrales dobles sobre regiones generales

En las integrales definidas anteriormente, la región de integración corresponde a un rectangulo sobre el plano $XY$, sin embargo se puede realizar integrales sobre regiones más generales definidas por curvas dependintes de $x$ (regiones tipo I) o curvas dependientes de $y$ (regiones tipo II).

A continuación se muestran las ecuaciones para calcular estas integrales.

Para regiones tipo I:

$D={(x,y) \in a \le x \le b, g_1(x) \le y \le g_2(x)}$

$\int_D{f(x,y)dA}=\int_a^b\int_{g_1(x)}^{g_2(x)}{f(x,y)dydx}$

Para regiones tipo II:

$D={(x,y) \in c \le y \le d, h_1(x) \le x \le h_2(x)}$

$\int_D{f(x,y)dA}=\int_c^d\int_{h_1(x)}^{h_2(x)}{f(x,y)dxdy}$

También es importante notar que una región más general se puede partir y obtener la integral como la suma de las integrales así:

Si $D = D_1 \cup D_2$ entonces:

$\iint_D{f(x,y)dA}=\iint_{D_1}{f(x,y)dA}+\iint_{D_2}{f(x,y)dA}$

4.1. Integrales dobles en coordenadas polares

Para realizar una integral en coordenadas polares puede utilizarse el siguiente cambio de variable:

Si $f$ es continua en un rectangulo polar dado por $R$ tal que $0 \le a \le r \le b$ y $\alpha \le \theta \le \beta$ y $0 \le \beta – \alpha \le 2 \pi$ entonces:

$\iint_R{f(x,y)dA}=\int_\alpha^\beta\int_a^b{f(r\cos\theta,r\sin\theta)rdrd\theta}$

Note que también puede integrar sobre funciones que definan los arcos similar al caso de integrales sobre regiones generales en coordenadas rectangulares.

5. Aplicaciones de Integrales dobles

Algunas de las aplicaciones más comunes de integrales dobles se muestran a continuación, estas aplicaciones fácilmente pueden ser extendidas a más de dos dimensiones utilizando integrales triples.

5.1. Masa

Dada la densidad, que es la masa por unidad de área y si esta densidad es variable se puede utilizar esta definición para calcular la masa usando:

$m=\iint_D{\rho(x,y)dA}$

5.2. Momentos

Los momentos de masa se pueden entender desde su aplicación que permite obtener el centro de masa de una lámina, estos centros de masa equivalen al punto donde la lámina se equilibra y es equivalente a tener toda la mas ubicada en ese punto, a continuación se dan las ecuaciones de los momentos y centros de masa de una lámina con densidad variable.

$M_x=\iint_D{y\rho(x,y)dA}$

$M_y=\iint_D{x\rho(x,y)dA}$

Y el centro de masa:

$\bar x=\frac{1}{m}\iint_D{x\rho(x,y)dA}$

$\bar y=\frac{1}{m}\iint_D{y\rho(x,y)dA}$

Los segundos momentos son conocidos así pues representan el momento de inercia de la lámina, a continuación se muestran estos momentos respecto a los ejes y al origen, este último también se conoce como momento polar de inercia:

$I_x=\iint_D{y^2\rho(x,y)dA}$

$I_y=\iint_D{x^2\rho(x,y)dA}$

$I_0=\iint_D{(x^2+y^2)\rho(x,y)dA}$

5.2. Área Superficial

El área de una superficie se puede calcular con el uso de integrales dobles, si tenemos la representación paramétrica de la superficie:

$\mathbf r=x(u,v)\mathbf i + y(u,v) \mathbf j + z(u,v) \mathbf k$

Entonces el área superficial esta definida por:

$A(S)=\iint_D{1\mathbf r_u \times \mathbf r_v| dA}$

Donde

$\mathbf r_u=\frac{\partial x}{\partial u}\mathbf i + \frac{\partial y}{\partial u} \mathbf j + \frac{\partial z}{\partial u} \mathbf k$

$\mathbf r_v=\frac{\partial x}{\partial v}\mathbf i + \frac{\partial y}{\partial v} \mathbf j + \frac{\partial z}{\partial v} \mathbf k$

Alternativamente se puede calcular como:

$A(S)=\iint_D{\sqrt{1+\frac{\partial z}{\partial x}^2+\frac{\partial z}{\partial y}^2}dA}$

6. Integrales triples

Las integrales triples son muy parecidas a las integrales dobles excepto que existe una variable adicional, además aplican las mismas reglas y principios. En este caso no existe una interpretación gráfica como tal ya que la región de integración es un volumen y se esta integrando una función de tres variables cuyos valores se requerirían dibujar en el hiperespacio cuadridimensional.

El teorema de Fubini aplica de igual manera y las regiones de integración no necesariamente deben ser cubos, sino que pueden ser funciones que acoten la región.

En general la integral de tres variables se define con sumas de Reimann y se puede escribir como:

$\iiint_B{f(x,y,z)dV}=\int_r^s\int_c^d\int_a^b{f(x,y,z)dxdydz}$

Para regiones generales se puede establecer integrales como la siguiente:

$\iiint_B{f(x,y,z)dV}=\int_a^b\int_{g_1(x)}^{g_2(x)}\int_{u_1(x,y)}^{u_2(x,y)}{f(x,y,z)dxdydz}$

6.1. Integrales triples en coordenadas cilíndricas

El cambio de variable para coordenadas cilíndricas en integrales triples arroja el siguiente resultado:

$\iiint_B{f(x,y,z)dV}=\int_\alpha^\beta\int_{h_1(\theta)}^{h_2(\theta)}\int_{u_1(r\cos\theta,r\sin\theta)}^{u_2(r\cos\theta,r\sin\theta)}{f(r\cos\theta,r\sin\theta,z)rdzdrd\theta}$

6.2. Integrales triples en coordenadas esféricas

El cambio de variable para coordenadas esféricas en integrales triples arroja el siguiente resultado:

$\iiint_B{f(x,y,z)dV}=\int_c^d\int_\alpha^\beta\int_a^b{f(\rho\sin\phi\cos\theta,\rho\sin\phi\sin\theta,\rho\cos\phi)\rho^2\sin\phi d\rho d\theta d\phi}$

7. Cambio de variables y Jacobiano

La transformación o cambio de una variable cuando la integral es de una sola variable se puede realizar de la siguiente manera:

$\int_a^b{f(x)dx}=\int_c^d{f(g(u))g'(u)du}$

La equivalencia entre los límites esta dada por $x=g(u)$ es decir $a=g(c)$ y $b=g(d)$.

En el caso de dos o más variables, también se puede realizar cambios de variables, como el de coordenadas polares, cilíndricas o esféricas. Para realizar este cambio debemos comprender que se esta transformando la región original de integración en una nueva y que para ello denotamos el nuevo plano y los nuevos límites con nombres de variables diferentes. Así mismo, definimos que una transformación $T$ es una $transformacion C^{-1}$ lo cual indica que las funciones de transformación $g$ y $h$ tienen derivadas parciales continuas.

$x=g(u,v)$

$y=h(u,v)$

Las nuevas variables son $u$ y $v$ y el la región original $R$ se llamará ahora $S$.

En general integrar realizando un cambio de variables en dos o más variables es conveniente definir el siguiente determinante que se conoce como el jacobiano:

$\frac{\partial (x,y)}{\partial (u,v)}=\left| \begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial x}{\partial v} \end{array} \right|=\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial x}{\partial v}\frac{\partial y}{\partial u}$

Con esta definición el cambio de variables en dos variables se puede escribir como:

$\iint_R{f(x,y)dA}=\iint_S{f(x(u,v),y(u,v))|\frac{\partial (x,y)}{\partial (u,v)}|dudv}$

8. Artículos de Interés

Geometría Vectorial

Sistemas de Coordenadas

Técnicas de Integración en Cálculo

Luego de estudiar las derivadas en una sola variable y en general el cálculo en una sola variables, la extensión natural surge cuando consideramos funciones de más de una variable y por lo tanto también aparece la posibilidad de obtener Derivadas Parciales en Varias Variables, las consideraciones más importantes se recopilan en este post.

Para aprender derivadas en una sola variable sigue este link.

1. Funciones varias variables

Las funciones de dos variables se representan como superficies en el espacio tridimensional y depende de dos variables. El dominio y el rango de estas funciones es similar al caso de funciones de una sola variable.

Alternativamente, las funciones de dos variables se pueden representar como curvas en el plano usando las denominadas curvas de nivel que son aquellas curvas para las cuales las funciones de dos variables asumen el mismo valor, esta aproximación es bastante usada en cartografía. Las curvas de nivel están dadas por:

$f(x,y)=k$

También pueden existir funciones de más de dos variables en cuyo caso no se puede obtener una representación gráfica, a lo sumo se puede obtener superficies de nivel y dibujar estas superficies en el espacio tridimensional.

2. Límites y Continuidad

En el caso de varias variables se puede expresar:

$\lim_{(x,y)\to {(a,b)}} f(x,y)=L$

Entonces podemos acercar el valor del límite a $L$ tanto como queramos, acercado lo suficiente $(x,y)$ a $(a,b)$ pero sin que sean iguales.

En el caso de varias variables hay una diferencia con una sola variable y es que para aproximarnos a un punto en el caso de una sola variable solo habían dos opciones o por la izquierda o por la derecha, sin embargo en el caso de varias variables tenemos infinitas opciones o trayectorias, un límite no existe si los valores de los límites por trayectorias diferentes difieren. Dado que no es posible demostrar que un límite exista para todas las trayectorias, se pueden usar alternativas como el teorema del emparedado para demostrar la existencia de estos límites.

Adicionalmente, si el límite existe en un punto $(a,b)$ se dice que la función es continua. Hay que tener presente que la función también puede ser continua en todo el dominio o un subconjunto del dominio.

3. Derivadas parciales

Para realizar una derivada parcial de una función $f(x,y)$ respecto de $x$ simplemente se debe derivar siguiendo las mismas reglas del caso de una variable y tomando $y$ como constante, en este caso se encontrará la pendiente de la superficie y el plano reticular $x$. Similarmente se puede realizar la derivada parcial respecto a $y$.

Para representar la derivada parcial de $x$ se puede usar las siguientes notaciones

$f_x(x,y)=f_x=\frac{\partial f}{\partial x}=\frac{\partial}{\partial x}f(x,y)=\frac{\partial z}{\partial x}=f_1=D_1f=D_xf$

En el caso de más de dos variables la derivada parcial opera en la misma forma que este caso, se toma la variable respecto de la cual se desea derivar y se dejan fijas el resto de variables.

También es posible realizar derivadas de orden superior simplemente tomando la derivada correspondiente del resultado previo de derivar. Las derivadas de orden superior se pueden escribir así:

$(f_x)_x=f_{xx}=f_{11}=\frac{\partial}{\partial x}\frac{\partial f}{\partial x}=\frac{\partial^2f}{\partial x^2}$

Cuando aparecen las derivadas de orden superior o segundas derivadas es posible que nos encontremos con las diferentes combinaciones de derivación entre las variables $x$ y $y$, por ejemplo, aquí se muestra la derivada cruzada primero derivando en $x$ y luego en $y$

$(f_x)_y=f_{xy}=f_{12}=\frac{\partial}{\partial y}\frac{\partial f}{\partial x}=\frac{\partial^2f}{\partial y \partial x}$

3.1. Teorema de Clairaut

Este teorema establece una igualdad entre las derivadas cruzadas, siendo $f$ una función continua en un disco $D$ entonces se cumple que:

$f_{xy}=f_{yx}$

3.2. Regla de la cadena en varias variables

La regla de la cadena en varias variables se puede escribir con los siguientes dos casos:

Caso 1:

Una función $z=f(x,y)$ es una función diferenciable de $x$ y $y$, donde $x=g(t)$ y $y=h(t)$ son funciones diferenciables de $t$ Entonces $z$ es una función diferenciable de $t$:

$\frac{dz}{dt}=\frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{dy}{dt}$

Caso 2:

Sea la función $z=f(x,y)$ es una función diferenciable de $x$ y $y$ donde $x=g(s,t)$ y $y=h(s,t)$ son funciones diferenciables de $s$ y $t$:

$\frac{\partial z}{\partial s}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial s}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial s}$

$\frac{\partial z}{\partial t}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial t}$

3.3. Diferenciación implícita

La regla de la cadena permite obtener ecuaciones sencillas para derivadas complejas, se puede obtener la derivada de $y$ respecto a $x$ usando

$\frac{dy}{dx}=-\frac{F_x}{F_y}$

4. Aproximaciones lineales

En el cálculo de una variable una de las ideas más importantes es que a medida que nos acercamos a un punto la gráfica se parece cada vez más a una línea recta lo cual permite obtener simplificaciones de funciones alrededor de ese punto. En el cálculo de varias variables sucede lo mismo, excepto que la aproximación esta dada por un plano tangente y no por una recta.

Si $f$ tiene derivadas parciales continuas, una ecuación del plano tangente a la superficie $z=f(x,y)$ en el punto $P_0$ es:

$z-z_0=f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)$

A $z$ en la ecuación anterior se le conoce como linealización o aproximación lineal o plano tangente de aproximación de la función $f$.

De la linealización se puede obtener que:

Si las derivadas parciales $f_x$ y $f_y$ existen cerca de $(a,b)$ y son continuas en $(a,b)$ entonces $f$ es diferenciable en $(a,b)$

4.1 Planos tangentes y superficies paramétricas

En el caso que la función (superficie) sea descrita por sus ecuaciones paramétricas:

$\mathbf r(u,v) = x(u,v)\mathbf i+ y(u,v)\mathbf j + z(u,v)\mathbf k$

en el punto $P_0$ dado por $\mathbf r(u_0,v_0)$ se puede obtener dos vectores tangentes a este punto usando derivadas parciales

Con $\mathbf r(u_o,v)$

$\mathbf r_v=\frac{\partial x}{\partial v}(u_0,v_0)\mathbf i + \frac{\partial y}{\partial v}(u_0,v_0)\mathbf j + \frac{\partial z}{\partial v}(u_0,v_0)\mathbf k$

Con $\mathbf r(u,v_0)$

$\mathbf r_v=\frac{\partial x}{\partial u}(u_0,v_0)\mathbf i + \frac{\partial y}{\partial u}(u_0,v_0)\mathbf j + \frac{\partial z}{\partial u}(u_0,v_0)\mathbf k$

Si $\mathbf r_u \times \mathbf r_v$ no es \mathbf 0$ se dice que la superficie es suave y un plano tangente contiene estos dos vecores.

5. Derivadas direccionales y Vector gradiente

Hasta el momento las derivadas parciales han sido respecto a una de las variables independientes de la función. Es posible calcular la derivada en cualquier dirección, no solamente en las direcciones de $x$ o $y$ para ello es necesario contar con el vector unitario que da la dirección en la cual queremos calcular la derivada $\mathbf u = $. En este caso se obtendra la pendiente de la superficie cortada por la reticula en la dirección del vector.

Para calcular la derivada direccional se puede realizar con la siguiente fórmula:

$D_uf(x,y)=f_x(x,y)a+f_y(x,y)b$

El vector gradiente, es un vector especial y muy utilizado en cálculo vectorial y se define como:

$\nabla f(x,y)=\frac{\partial f}{\partial x}\mathbf i + \frac{\partial f}{\partial y}\mathbf j$

Con esta notación podemos reescribir la derivada direccional usando el vector gradiente el producto punto:

$D_uf(x,y)=\nabla f(x,y) \cdot \mathbf u$

La importancia del vector gradiente es debido a que la dirección del vector gradiente corresponde a la mpaxima velocidad de cambio de la superficie correspondiente. Otro hecho destacable es que el vector gradiente es perpendicular a la curva de nivel (o superficie de nivel en el caso de una función de tres variables).

6. Valores Máximos y Mínimos

Una función $f$ tiene un valor máximo o mínimo local en $(a,b)$ y existen las derivadas parciales de primer orden de $f$ entonces $f_x(a,b)=0$ y $f_y(a,b)=0$

En el caso que se cumpla que ambas derivadas sean cero o que alguna de ellas no exista se llama a este un punto crítico o estacionario.

También se puede obtener mediante la prueba de la segunda derivadas información para clasificar los máximos y los mínimos. Si las segundas derivadas son continuas en un disco con centro en $(a,b)$ y este es un punto crítico; sea:

$D=D(a,b)=f_{xx}(a,b)f_{yy}(a,b)-(f_{xy})^2$

• Si $D>0$ y $f_{xx}(a,b)>0, entonces $f(a,b)$ es un mínimo local.
• Si $D>0$ y $f_{xx}(a,b)<0, entonces $f(a,b)$ es un máximo local.
• Si $D<0$ entonces $f(a,b)$ es un punto de silla.

6.1. Máximos y mínimos absolutos

El teorema del valor extremo para funciones de dos variables establece que si $f$ es continua en un conjunto cerrado y acotado $D$ en $\mathbb R^2$ entonces $f$ tiene un máximo y un mínimo absoluto en algunos puntos de $D$.

Para hallar los valores máximos y mínimos absolutos, es suficiente con encontrar los valores máximos y mínimos correspondientes a los puntos críticos y luego hallar los valores correspondientes a los puntos sobre la frontera $D$, el mayor será el máximo absoluto y el menor será el mínimo absoluto.

7. Multiplicadores de Lagrange

Los multiplicadores de Lagrange es una técnica que permite encontrar el máximo y mínimo de una función $f(x,y,z)$ limitada por otra $g(x,y,z)=k$ para ello se debe resolver el sistema de ecuaciones:

$\nabla f(x,y,z)=\lambda \nabla g(x,y,z)$

$g(x,y,z)=k$

En este caso $k$ es el valor de la superficie que limita la función $f$

Una extensión de este método usando dos restricciones implica que el sistema de ecuaciones simultaneas sea:

$\nabla f(x,y,z)=\lambda \nabla g(x,y,z) + \mu \nabla h(x,y,x)$

$g(x,y,z)=k$

$h(x,y,z)=c$

8. Artículos de Interés

Funciones de dos variables y Superficies

Límites en Cálculo

Derivadas en Cálculo