Sistemas de Coordenadas

Los Sistemas de Coordenadas son muy útiles ya que de su correcta elección un problema puede resolverse fácilmente o por el contrario puede resultar muy complejos o casi imposible. Este post contiene las diferentes equivalencias que existen entre los Sistemas de Coordenadas más comunes.

Tenga presente que existen otros sistemas de coordenadas como parabólicas, paraboloidales, elípticas, eferoidales alargadas y achatadas, bipolares, toroidales, cónicas, entre otras.

Si quieres aprender a programar este es un buen lugar para iniciar.

1. Coordenadas en 2D

1.1. Coordenadas rectangulares

Las coordenadas rectangulares especifica un punto en el plano usando las distancias a los ejes coordenados como se muestra en la figura siguiente.

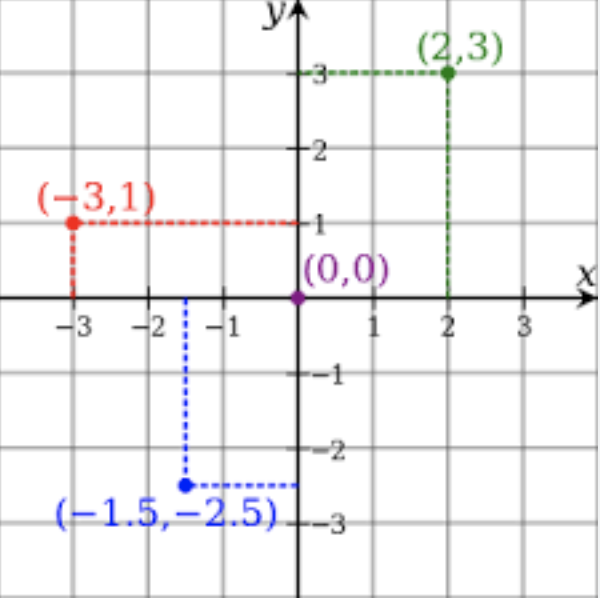
Las ecuaciones para convertir del sistema rectangular a sistema polar son las siguientes.

$r^2=x^2+y^2$

$tan \theta = \frac{y}{x}$

1.2. Coordenadas Polares

las coordenadas polares especifican un punto en el plano usando las distancias al origen y el ángulo que forma el vector desde el origen al punto en cuestión tal y como se muestra en la figura siguiente.

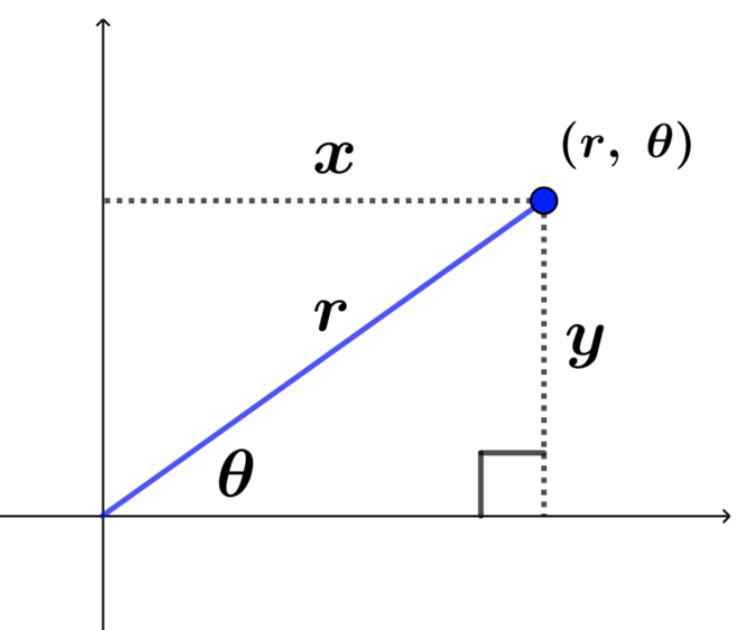
Las ecuaciones para convertir del sistema polar al sistema rectangular son las siguientes.

$x=r\cos\theta$

$y=r\sin\theta$

2. Coordenadas en 3D

2.1. Coordenadas Rectangulares

Este caso es la extensión del sistema rectangular en 2D agregando la profundidad en el eje $z$ como se muestra en la siguiente figura.

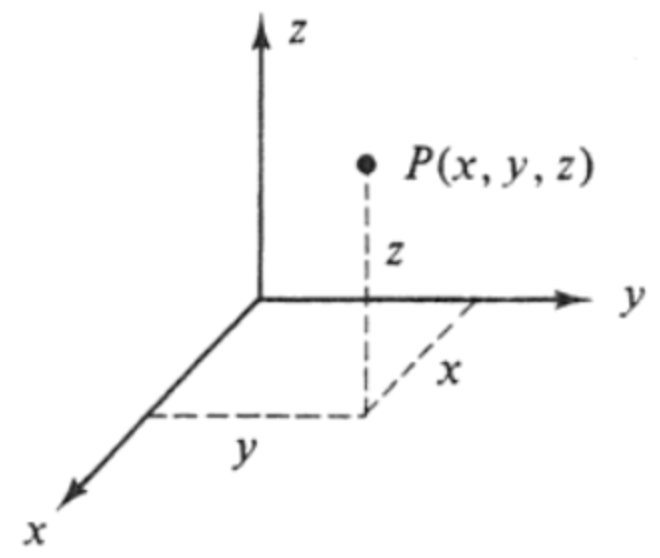
Para convertir coordenadas rectangulares en cilíndricas usamos las siguientes ecuaciones.

$r^2=x^2+y^2$

$tan \theta = \frac{y}{x}$

$z=z$

Para convertir coordenadas rectangulares en esféricas usamos las siguientes ecuaciones.

$r^2=x^2+y^2+z^2$

$\tan\phi=\frac{y}{x}$

$\cos\theta=\frac{z}{\sqrt{x^2+y^2+z^2}}$

2.2. Coordenadas Cilíndricas

Este caso es la extensión del sistema polar en 2D agregando la profundidad en el eje $z$ como se muestra en la siguiente figura.

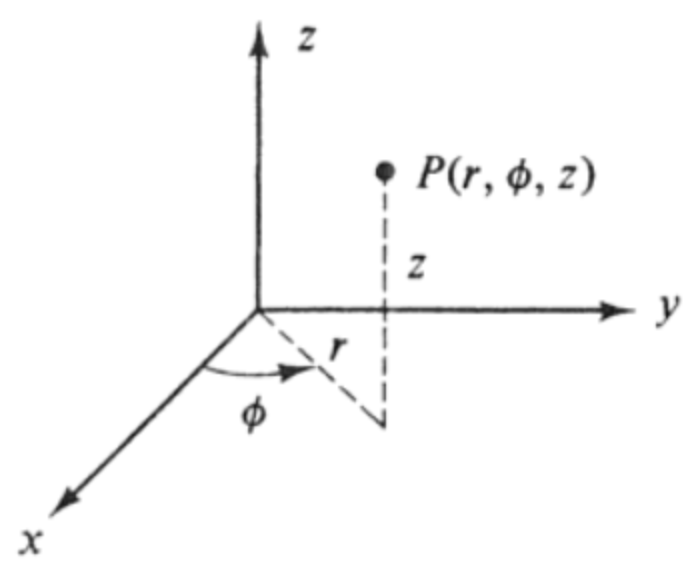
Las ecuaciones para convertir de coordenadas cilíndricas a coordenadas rectangular son las siguientes.

$x=r\cos\theta$

$y=r\sin\theta$

$z=z$

2.3. Coordenadas Esféricas

Estas coordenadas se construye con base a los ángulos que se forman entre el vector posición (entre el origen y el punto) y los diferentes ejes coordenados y la longitud del vector tal y como se muestra en la siguiente figura.

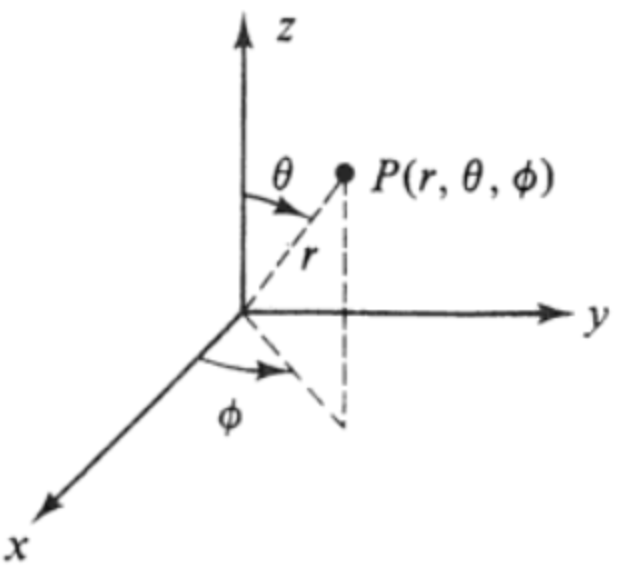
Las ecuaciones para convertir de coordenadas esféricas a sistema rectangular son las siguientes.

$x=\rho\sin\phi\cos\theta$

$y=\rho\sin\phi\sin\theta$

$z=\rho\cos\phi$

3. Artículos de Interés

Geometría Vectorial

Funciones de dos variables y Superficies

Integrales en Cálculo