Las funciones de dos variables son una extensión de las funciones de las funciones de una sola variable que se estudian en este post. Adicionalmente, las Funciones de dos variables y Superficies correspondientes son comúnmente utilizadas en una sin fin de aplicaciones practicas.
Generalidades de las Funciones de una variable
1. Definición de Funciones de dos variables
Las Funciones de dos variables y Superficies son análogas a las funciones de una sola variable y por lo tanto aplican los mismos conceptos como Dominio y Rango.
En este caso se puede representar la función de la siguiente manera:
$f(x,y)=z$
Donde $z$ es la función de las variables independientes $x$ y $y$ el dominio $D$ y el rango el conjunto de valores que puede tomar $f$ es decir ${f(x,y)|(x,y) \in D}$
2. Gráficas de Funciones de dos variables
Las gráficas de estas funciones pueden realizarse en $\mathbb R^3$ de tal manera que:
$z=f(x,y)$ y $(x,y) \in D$
Así como en el caso de una sola variable era muy conveniente tener la representación de la línea recta, en el caso de dos dimensiones es muy útil la extensión de este concepto para obtener funciones lineales que son planos en $\mathbb R^3$, la función lineal es la siguiente
$f(x,y)=ax+by+c$
Algunas gráficas importantes se muestran a continuación, así como las denominadas superficies cuadráticas que se obtiene de las diferentes combinaciones de las esfera.
2.1. Cilindro parabólico
Esta gráfica esta dada por la ecuación:
$f(x,y)=x^2$
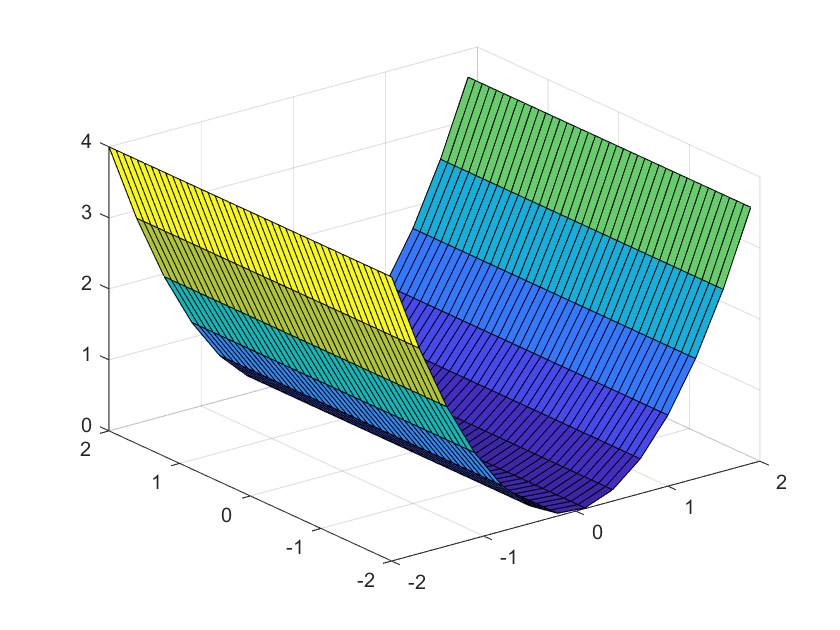
2.2. Paraboloide elíptico
Esta gráfica de una superficie cuadrática esta dada por la ecuación:
$\frac{z}{c}=\frac{x^2}{a^2}+\frac{y^2}{b^2}$
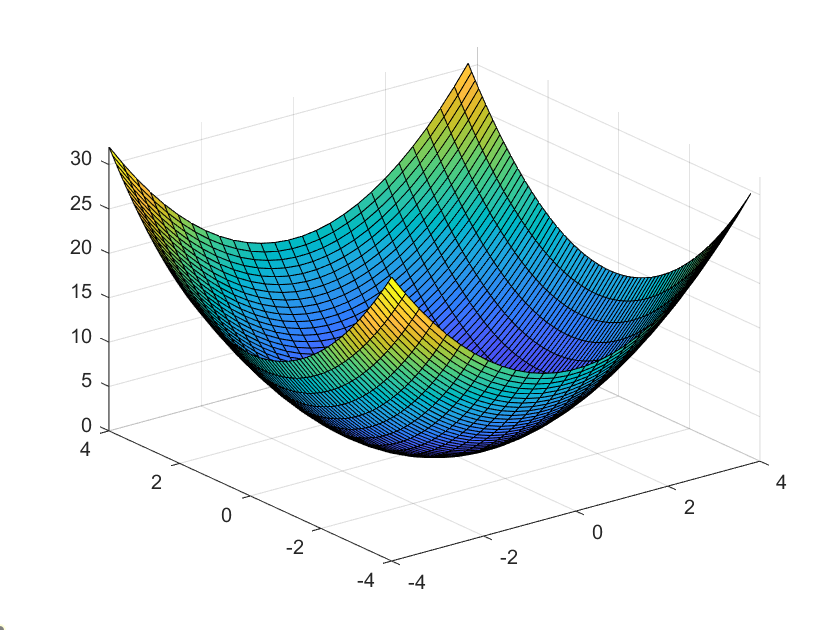
2.3. Paraboloide hiperbólico
Esta gráfica de una superficie cuadrática esta dada por la ecuación:
$\frac{z}{c}=\frac{x^2}{a^2}-\frac{y^2}{b^2}$
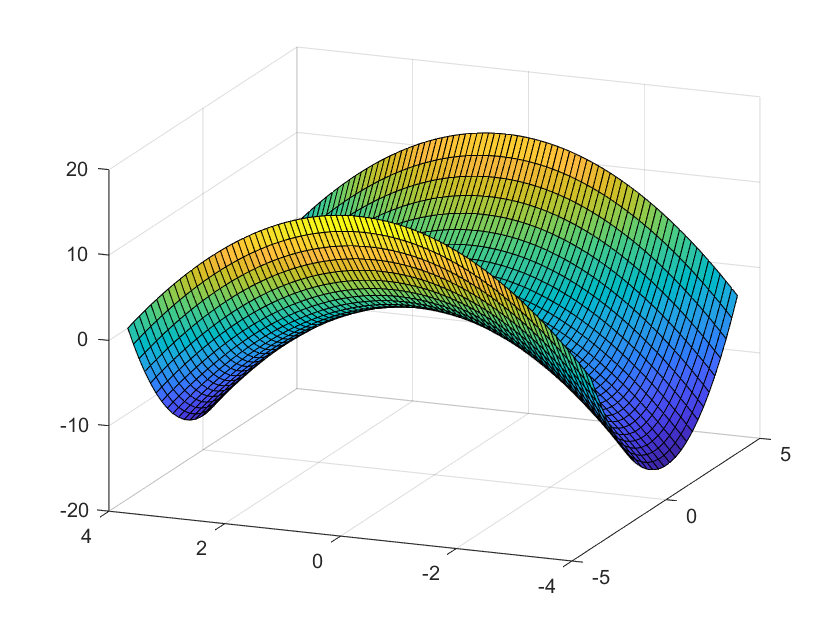
2.4. Elipsoide
Esta gráfica de una superficie cuadrática esta dada por la ecuación:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$
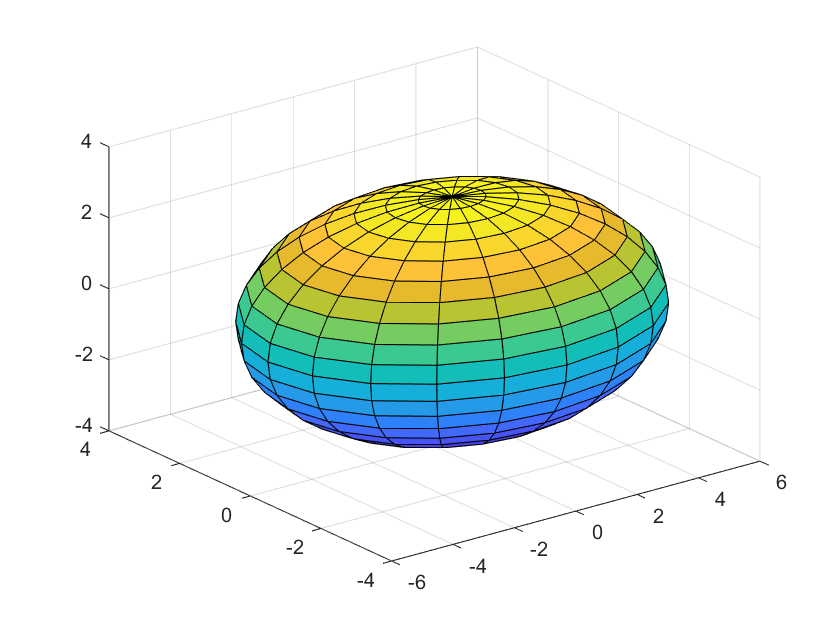
2.5. Cono
Esta gráfica de una superficie cuadrática esta dada por la ecuación:
$\frac{z^2}{c^2}=\frac{x^2}{a^2}+\frac{y^2}{b^2}$
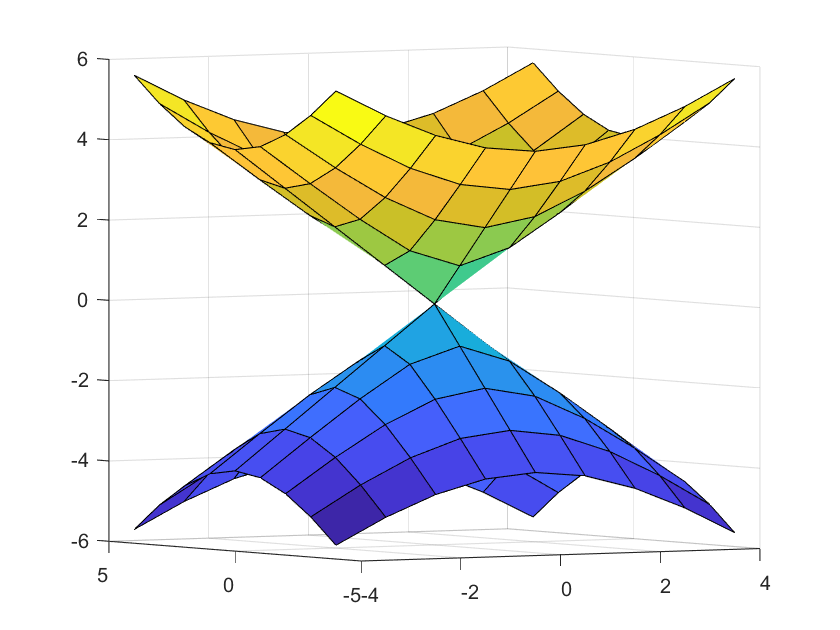
2.6. Hiperboloide de una hoja
Esta gráfica de una superficie cuadrática esta dada por la ecuación:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$
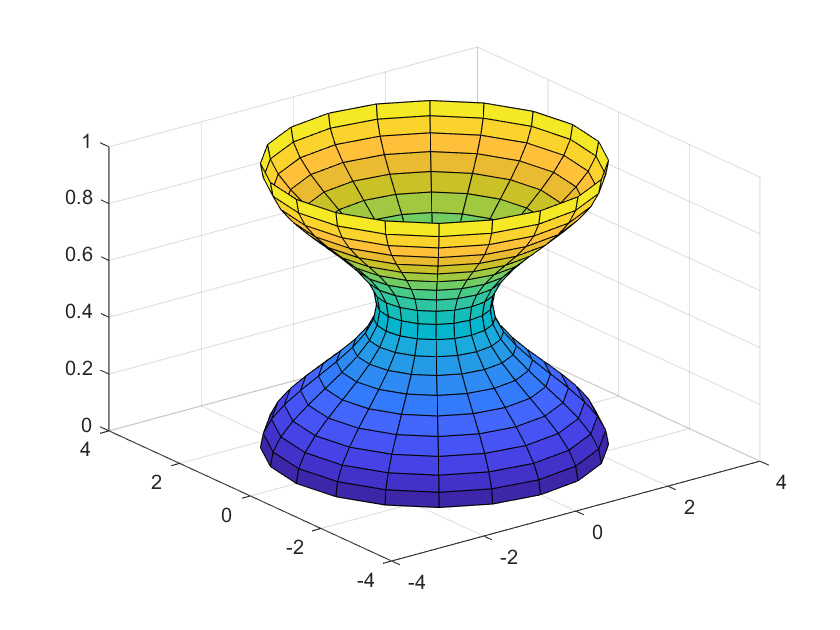
2.7. Hiperboloide de dos hojas
Esta gráfica de una superficie cuadrática esta dada por la ecuación:
$-\frac{x^2}{a^2}-\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$
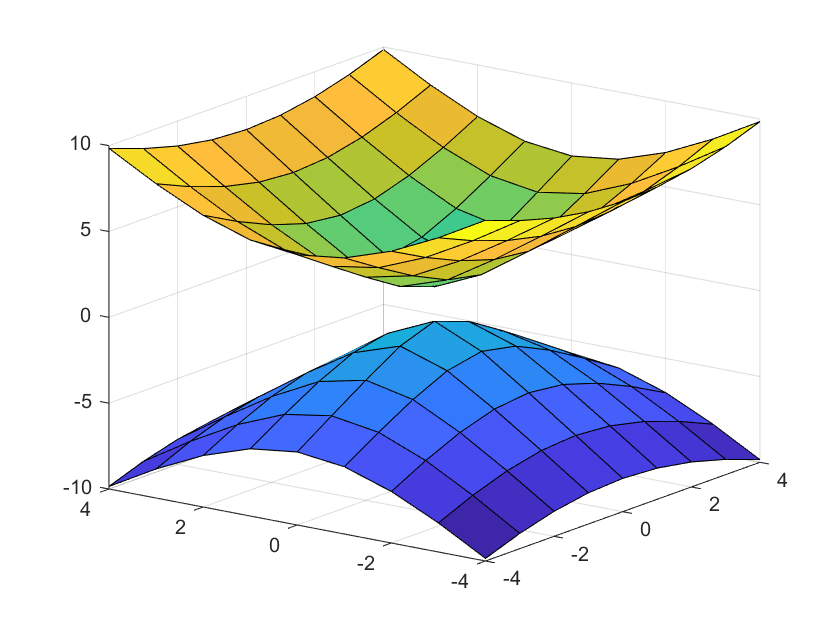
2.8. Esfera
Esta gráfica de una superficie cuadrática esta dada por la ecuación:
$z^2+x^2+y^2=r^2$
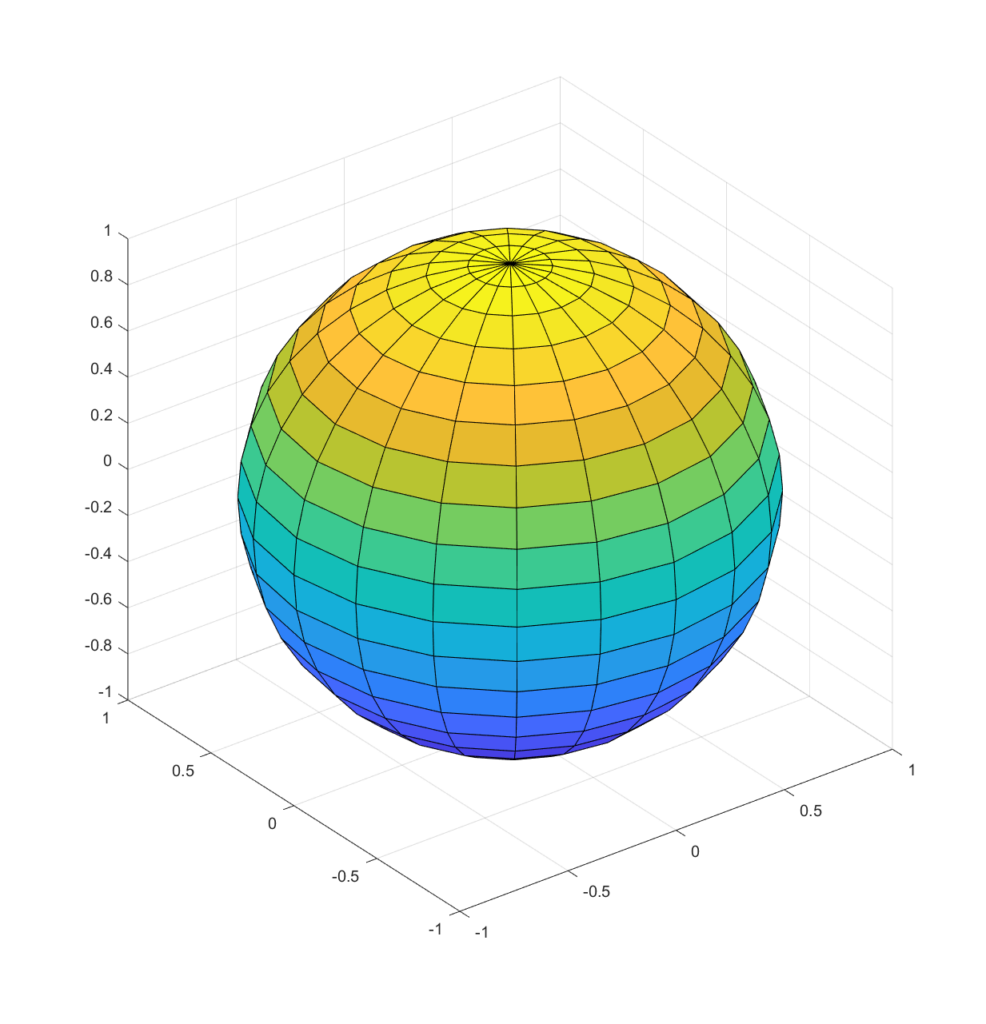
2.9. Otras funciones
La siguiente gráfica esta dada por la ecuación:
$f(x,y)=(x^2+4y^2)e^{-x^2-y^2}$
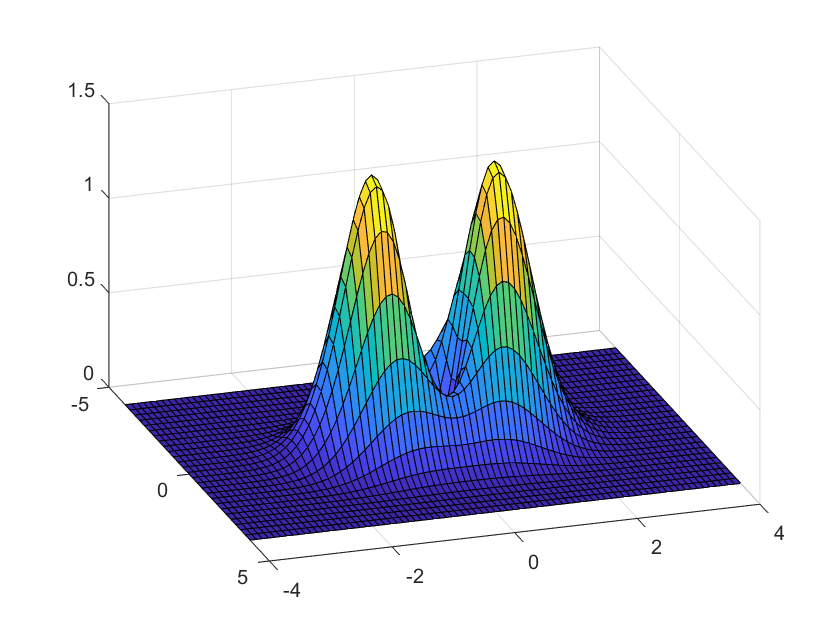
La siguiente gráfica esta dada por la ecuación:
$f(x,y)=\sin{x}+\sin{y}$
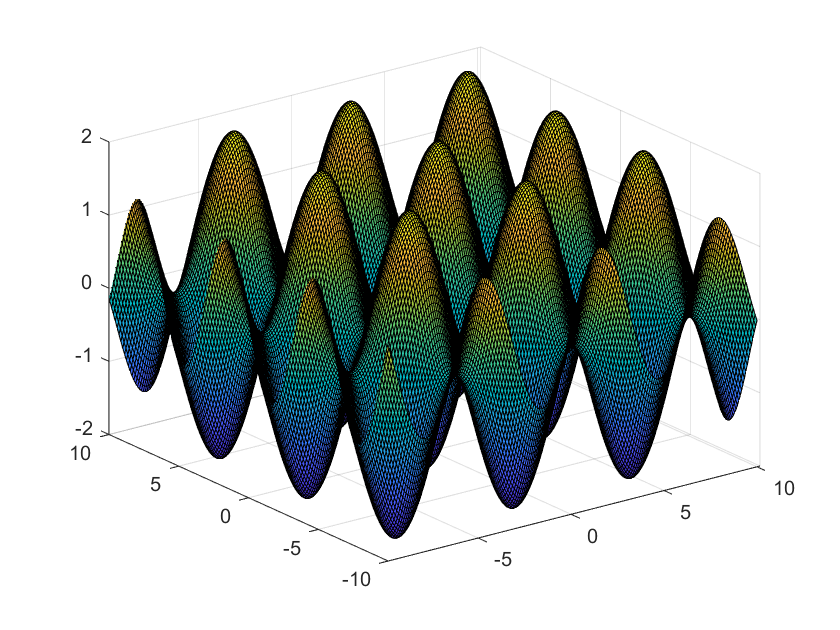
La siguiente gráfica esta dada por la ecuación:
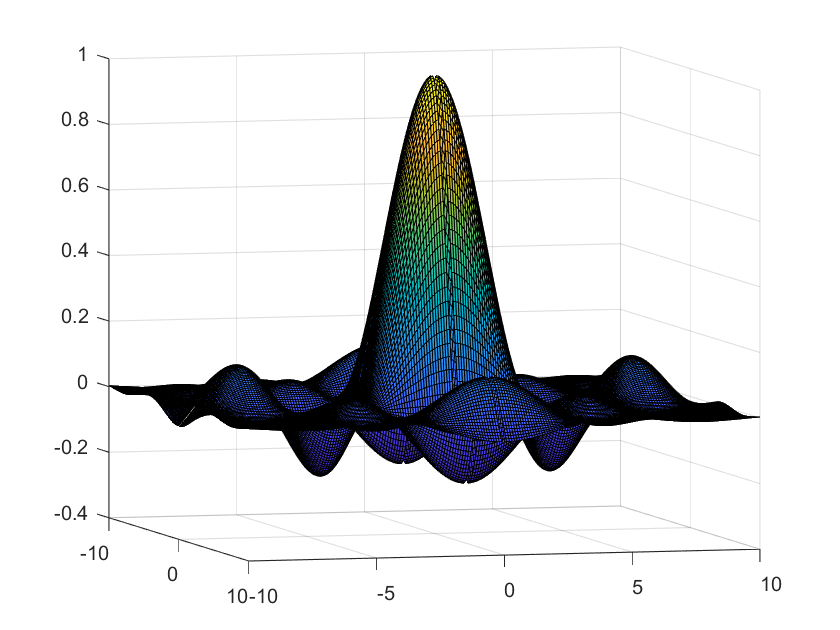
$f(x,y)=\frac{\sin{x}\sin{y}}{xy}$


Deja un comentario
Lo siento, debes estar conectado para publicar un comentario.