En estas páginas encontraras el material necesario para comprender las diferentes Funciones Matemáticas, además de un catalogo completo con sus correspondientes usos y aplicaciones.
1. Generalidades de las funciones
Las funciones aparecen cuando existen cantidades que dependen unas de las otras, normalmente se ha definido una función como una regla que asigna a cada elemento $x$ de un conjunto $A$ exactamente un elemento llamado $f(x)$f de otro conjunto $B$. En este punto tenemos algunas definiciones convenientes que realizar en el manejo de las funciones:
- Dominio: este concepto corresponde al mismo conjunto $A$
- Rango: este concepto corresponde al mismo conjunto $B$
- Variable independiente: variable que representa un elemento arbitrario del conjunto $A$ (dominio)
- Variable dependiente: variable que representa un elemento en el rango de $f$
Las funciones matemáticas se pueden representar de distintas maneras incluyendo:
- Verbalmente (usando una descripción en prosa), numéricamente (con una tabla de valores)
- Visualmente (con una gráfica) o algebraicamente (con una fórmula o ecuación).
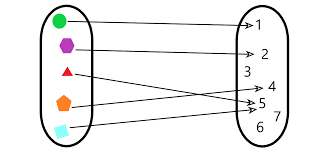
La última es la forma más habitual y conveniente para expresar funciones, así mismo se puede visualizar la función recurriendo a la visualización como regla de asignación entre conjuntos, más formalmente tendríamos que si $f$ es una función cuyo dominio es $A$ su gráfica son las parejas ordenadas
$\{(x,f(x))x \in A\}$
Y su correspondiente diagrama de flechas es como el de la figura 1.

1.1. Prueba de recta vertical
Ahora bien, es importante notar que la definición de función implica que la asignación del conjunto del dominio al conjunto del rango, no realice asignaciones de forma tal que un mismo elemento del dominio asigne dos valores diferentes del rango, gráficamente esto se puede ver fácilmente mediante la Prueba de la recta vertical de tal manera que si se traza una línea vertical en el gráfico de una función esta corte la gráfica en un solo punto. De tal manera, la gráfica 2 corresponde a una parabola pero no a una función.

1.2. Funciones por secciones
Otra forma de definir funciones es utilizando la definición de funciones matemáticas por secciones, de estas funciones la más conocida es la función valor absoluto, la cual se muestra en la figura 3. De esta forma se puede definir funciones de una manera muy flexible, por ejemplo la función escalón es una de ellas.

1.1. Simetría
Existen dos tipos de simetría para las Funciones Matemáticas, la simetría par y la simetría impar. La primera es cuando se cumple la condición f(−x)=f(x)f(-x)=f(x) y la segunda f(−x)=−f(x)f(-x)=-f(x), gráficamente se pueden observar estas simetrías siendo la simetría par una simetría respecto al eje yy en una gráfica en el plano cartesiano y la simetría impar una simetría respecto al origen en el plano cartesiano, las figuras 4 y 5 muestras estas simetrías respectivamente.


1.2. Funciones Matemáticas crecientes y decrecientes
Estas dos definiciones permiten ver el comportamiento de una función en un intervalo del dominio II, de tal manera que una función es
- Creciente: si se cumple que $f(x_1) \lt f(x_2)$ siempre que $x_1 \lt x_2$ en $I$
- Decreciente: si se cumple que $f(x_1) \gt f(x_2)$ siempre que $x_1 \gt x_2$ en $I$
Las gráficas 6 y 7 muestran respectivamente funciones crecientes y decrecientes.


2. Transformación de Funciones
Las transformaciones de Funciones Matemáticas son muy útiles, puesto que permiten construir funciones que a primera mano parecen muy complejas usando funciones básicas, lo anterior ayuda a imaginarnos las gráficas de las funciones con las que se trabaja fácilmente.
2.1. Desplazamientos verticales y horizontales
A continuación se listan los diferentes desplazamientos que se pueden realizar partiendo de una constante $c \gt 0$ y la función $y=f(x)$
- Hacia abajo: $y=f(x)−c$
- Hacia arriba: $y=f(x)+c$
- Hacia la izquierda: $y=f(x+c)$
- Hacia la derecha: $y=f(x−c)$
2.2. Alargamientos y reflexiones
A continuación se listan los diferentes operaciones de alargamiento y compresión que se pueden realizar partiendo de una constante $c \gt 1$ y la función $y=f(x)$
- Alargamiento vertical: $y=cf(x)$
- Compresión vertical: $y=(\frac{1}{c})f(x)$
- Compresión horizontal: $y=f(cx)$
- Alargamiento vertical: $y=f(\frac{x}{c})$
- Reflexión respecto a x: $y=−f(x)$
- Reflexión respecto a y: $y=f(−x)$
2.3. Algebra de funciones
Las funciones se pueden operar usando los operadores algebraicos tradicionales para obtener nuevas funciones, de forma similar existe una operación llamada composición de funciones estas operaciones se muestran a continuación para las funciones $f(x)$ y $g(x)$
- Suma de funciones: $(f+g)(x)=f(x)+g(x)$ dominio $A \cap B$
- Resta de funciones: $(f−g)(x)=f(x)−g(x)$ dominio $A \cap B$
- Multiplicación de funciones: $(fg)(x)=f(x)g(x)$ dominio $A \cap B$
- División de funciones: $(\frac{f}{g})(x)=\frac{f(x)}{g(x)}$ dominio ${x \in A \cap B | g(x) \ne 0}$
- Composición de funciones: $f(u)=f(g(x))$ que también se escribe como $(f \circ g)(x)=f(g(x))$
3. Curvas paramétricas
En ocasiones las funciones pueden escribirse en términos de sus componentes en los ejes $x$ e $y$, para ellos se expresan en dos ecuaciones como sigue:
$x=f(t) \text{ ; } y=g(t)$
La variable $t$ se conoce como parámetro. Es importante notar que estas expresiones pueden dar lugar a un concepto más general que el de función debido a que si se despeja $t$ en las ecuaciones anteriores y se igualan el resultado puede no superar la prueba de la línea vertical y como consecuencia obtener una relación, para ello se utiliza el término más general curva. Considere como ejemplo el caso de las curvas paramétricas de un círculo de centro $(h,k)$ y radio $r$:
$x=h+r\sin(t) \text{ ; } y=k+r\cos(t)$
4. Funciones inversas
Antes de definir la función inversa, definamos una función uno a uno (ver correspondencia de funciones) como aquella función que nunca adopta el mismo valor dos veces:
$f(x_1) \ne f(x_2) \text{ siempre que } x_1 \neq x_2$
Otra forma de definir si una función es uno a uno es a través de la prueba de la recta horizontal, en este sentido una recta horizontal trazada sobre la gráfica de la función solamente la puede cortar una sola vez. Se define la función inversa siendo $f$ una función uno a uno con dominio $A$ y rango $B$, luego la función inversa $f^{−1}$ tiene rango $A$ y dominio $B$ y se define mediante:
$f^{-1}(y)=x \Leftrightarrow f(x)=y$
La función inversa implica las siguientes expresiones:
$f^{-1}(f(x))=x \text{ ; }\forall x \in A$
$f(f^{-1}(x))=x \text{ ; }\forall x \in B$
Para hallar la función inversa se debe resolver a xx en término de yy siempre y cuando sea posible.
5. Correspondencia de funciones
A continuación se estudia las principales correspondencias de funciones, como son: unívoca, biunívoca, inyectiva, biyectiva, sobreyectiva; las primeras correspondencias entre funciones (unívoca, biunívoca) tratan los conceptos más generales aplicados a conjuntos, pero también pueden entenderse desde el punto de vista de las funciones y en este caso las correspondencias se denominan aplicaciones, teniendo los casos inyectiva, biyectiva y sobreyectiva que se resumen a continuación. Considere $A$ el dominio de una función $f$ cuyo rango es $B$
5.1. Funciones inyectivas
Una función es inyectiva si a elementos diferentes del dominio asigna elementos diferentes del rango, formalmente las funciones inyectivas se definen como:
$a\text{ , }a’ \in A\text{ y }a \neq a’\text{ entonces }f(a) \neq f(a’)$
5.2. Funciones sobreyectivas
Las funciones sobreyectivas también son denominadas funciones suprayectivas, epiyectivas, suryectiva, exhaustiva o subyectivas y se definen como aquellas funciones que para todo número en el rango tienen un correspondiente valor en el dominio, formalmente se define como:
$\forall b \in B \text{ } \exists \text{ } a \in A \text{ con }f(a)=b$
La función también puede ser no sobreyectiva si la anterior premisa no se cumple.
6.3. Funciones biyectivas
Estas funciones también se denominan uno a uno, y son aquellas que son inyectivas y sobreyectivas al mismo tiempo.